Water enters into a smooth horizontal tapering tube with a speed 2 m/sec and emerges out of the tube with a speed 8 m/sec . Find the ratio of the radii of cross sections of the tube at these two ends.
To solve the problem, we will use the principle of continuity for fluid flow, which states that for an incompressible fluid, the product of the cross-sectional area and the velocity at one point is equal to the product at another point.
1. Identify Given Values:
- Velocity at the inlet (v1) = 2 m/s
- Velocity at the outlet (v2) = 8 m/s
2. Use the Equation of Continuity:
The equation of continuity states:
A1v1=A2v2
where A1 and A2 are the cross-sectional areas at the inlet and outlet, respectively.
3. Express Areas in Terms of Radii:
The area A of a circle is given by:
A=πr2
Therefore, we can express the areas at the two ends as:
A1=πr21andA2=πr22
4. Substitute Areas into the Continuity Equation:
Substituting the areas into the continuity equation gives:
πr21⋅v1=πr22⋅v2
The π cancels out:
r21v1=r22v2
5. Rearranging the Equation:
Rearranging the equation to find the ratio of the squares of the radii:
r21r22=v2v1
6. Substituting the Values of Velocities:
Substitute v1=2 m/s and v2=8 m/s:
r21r22=82=4
7. Taking the Square Root:
Taking the square root of both sides gives:
r1r2=√4=2
8. Final Ratio:
Therefore, the ratio of the radii of the cross sections of the tube at the two ends is:
r1:r2=2:1
- Velocity at the inlet (v1) = 2 m/s
- Velocity at the outlet (v2) = 8 m/s
The equation of continuity states:
A1v1=A2v2
where A1 and A2 are the cross-sectional areas at the inlet and outlet, respectively.
The area A of a circle is given by:
A=πr2
Therefore, we can express the areas at the two ends as:
A1=πr21andA2=πr22
Substituting the areas into the continuity equation gives:
πr21⋅v1=πr22⋅v2
The π cancels out:
r21v1=r22v2
Rearranging the equation to find the ratio of the squares of the radii:
r21r22=v2v1
Substitute v1=2 m/s and v2=8 m/s:
r21r22=82=4
Taking the square root of both sides gives:
r1r2=√4=2
Therefore, the ratio of the radii of the cross sections of the tube at the two ends is:
r1:r2=2:1
Topper's Solved these Questions
- FLUID MECHANICS Book:FIITJEEChapter:FLUID MECHANICS Exercise:ASSIGHNMENT PROBLEMS (SUBJECTIVE ) SHORT ANSWER TYPE QUESTIONS (LEVEL -I)
Explore 4 Videos
- FLUID MECHANICS Book:FIITJEEChapter:FLUID MECHANICS Exercise:ASSIGHNMENT PROBLEMS (SUBJECTIVE ) FILL IN THE BLANKS (LEVEL -I)
Explore 5 Videos
- FLUID MECHANICS Book:FIITJEEChapter:FLUID MECHANICS Exercise:MATRIX MATCH TYPES
Explore 6 Videos
- ELECTROSTATICSBook:FIITJEEChapter:ELECTROSTATICSExercise:Example
Explore 14 Videos
- GENERAL PHYSICSBook:FIITJEEChapter:GENERAL PHYSICSExercise:MATRIX MATCH TYPE
Explore 3 Videos
Similar Questions
The pressure difference between two points along a horizontal tube through which water is flowing is 2.5 cm of mercury. Calculate the speed of water at a point of smaller cross section if the speed at a point of larger cross section is 2.61 ms−1.
View SolutionWater is flowing through two capillary tubes under constant pressure head. The ratio of their lengths is 3:1 and of diameters is 2 : 1. Find the ratio of rate of flow of water through two tubes.
View Solution
Knowledge Check
An alpha particle enters a hollow tube of 4m length with an initial speed of 1km/s. It is accelerated in the tube and comes out of it with a speed of 9km/s. The time for which it remains inside the tube is
A8×10−3sB80×10−3sC800×10−3sD8×10−4sWhen two capillary tubes A and B are immersed in water , the heights of water columns are found to be in the ratio 2:3 the ratio of the radii of tubes A and B is
A2:3B4:9C9:4D3:2A horizontal jet of water coming out of a pipe of area of cross-section 20cm2 hits a vertical wall with a velocity of 10ms−1 and rebounds with the same speed. The force exerted by water on the wall is .
Athe thrust exerted by the water on the wall will be doubledBthe thrust exerted by the water on the wall will be four timesCthe energy lost per second by water strikeup the wall will also be four timesDthe energy lost per second by water striking the wall be increased eight times.
Water is flowing through a horizontal tube having non-uniform area of cross section. If pressure difference between two points along a horizontal tube is 1.5 cm of mercury and speed of flow of water at a point of smaller cross section is 3ms−1, then find the speed of water flow at the other point of larger cross section. Take g=10 m/s2.
View SolutionWater is flowing in a horizontal pipe ofnonuniform cross section. The velocities of water at points A and Bin the tube, are in the ratio of 4 : 1, what is the ratio of the diameters of the pipe at A and B ?
View SolutionWater is flowing through a tube of radius r with a speed v. If this tube is joined to another tube of radius r/2, what is the speed of water in the second tube?
View SolutionA glass tube has several different cross-sectional areas with the values indicated in the figure . A piston at the left end of the tube exerts pressure so that mercury within the tube flows from the right end with a speed of 8.0 m/s . Three points with in the tube are labeled A , B and C . (Atmospheric pressure is 1.01×105N/m2 , Density of mercury is 13600kg/m3) .
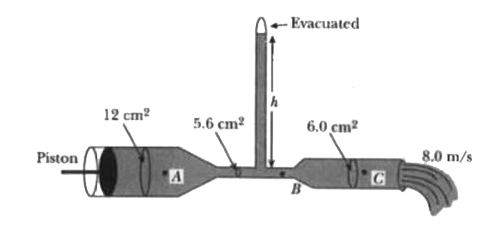
At what speed is mercury flowing past the point labeled B ?
View SolutionA glass tube has several different cross-sectional areas with the values indicated in the figure . A piston at the left end of the tube exerts pressure so that mercury within the tube flows from the right end with a speed of 8.0 m/s . Three points with in the tube are labeled A , B and C . (Atmospheric pressure is 1.01×105N/m2 , Density of mercury is 13600kg/m3) .
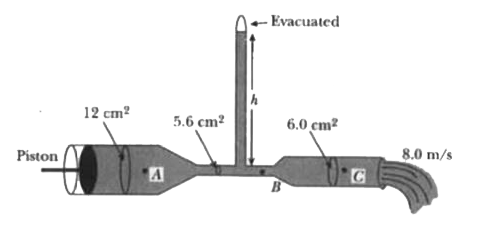
At what speed is mercury flowing past the point labeled A ?
View Solution

