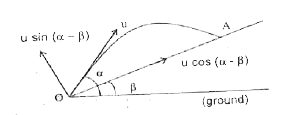
A particle is projected up an inclined plane of inclination $β$ at na elevation $\propto$ to the horizontal. Show that
(a) $tan \propto = cot β + 2 tan β$ , if the particle strikes the plane at right angles
(b) $tan \propto = 2 tan β$ , if the particle strikes the plane horizontally.

Video Solution

Text Solution

Verified by Experts

(a) Let be the time of flight from O to A
Then $t = \frac{2 u sin (α - β)}{g cos β}$
Now we shall consider the motion of (ground) the particle along OA.
Here initial velocity = u cos $(α - β)$
Final velocity = 0
(The particle strikes the plane A atright angles
Acceleration of the partide along the incline plane, due to gravity = -g sin $β$
$0 = u cos (α - β) - g sin β t$
or t = $\frac{u cos (α - β)}{g sin β}$
From equation (1) & (2) $\frac{2 u sin (α - β)}{g cos β}$ = $\frac{u cos (α - β)}{g sin β}$
or, 2 tan $(α - β)$ = cot $β$
or, $2 (\frac{tan α - t h a n β}{1 + t e n α tan β}) - cot β$
or , $2 tan α - 2 tan β cot β + tan α$
or, $tan α cot β + 2 tan β$
(b) When the particle strikes the plane, horizontally i.e. along the ground In this case, $t = \frac{2 u sin (α - β)}{g cos β}$
and 0 = u sin $α - >$
or u sin $α = g [\frac{2 u sin (α - β)}{g cos β}]$
or, sin $α cos β$ = 2 [ sin $α cos β - cos α sin β]$
or $2 cos α sin β = sin α cos β$
$\Rightarrow 2 tan β = tan α$

Updated on:21/07/2023

A particle is projected with a certain velocity at an angle $\propto$ above the horizontal from the foot of an inclined plane of inclination $30^{\circ}$ . If the particle strikes the plane normally, then $\propto$ is equal to.
A $30^{\circ} + {tan}^{- 1} (\frac{\sqrt{3}}{2})$
B $45^{\circ}$
C $60^{\circ}$
D $30^{\circ} + {tan}^{- 1} (2 \sqrt{3})$
A particle is projected with a certain velocity at an angle $α$ above the horizontal from the foot of an inclined plane of inclination $30^{\circ}$ . If the particle strikes the plane normally then $α$ is equal to
A $30^{\circ} + {tan}^{- 1} (\frac{\sqrt{3}}{2})$
B $45^{\circ}$
C $60^{\circ}$
D $30^{\circ} + {tan}^{- 1} (2 \sqrt{3})$
A particle is projected with a velocity u from the foot of an inclined plane whose inclination to the horizon is $β$ . It strikes. the plane at right angles if
A $tan (α - β) = cot β$
B $2 tan (α - β) = cot β$
C $2 cot (α - β) = cot β$
DNone of these