Let l be the moment of inertia of a uniform square plate about an axis AB that passes through its centre and is parallel to two of its sides. CD is a line in the plane of the plate that passes through the centre of the plate and makes an angle θ with AB. The moment of inertia of the plate about the axis CD is then equal to
I
I sin2θ
Icos2θ
Icos2(θ2).
The correct Answer is:A
In the figure, A′B′ is perpendicular to AB
C′D′ is perpendicular to CD
By symmetry, IAB=IA′B′
ICD=IC′D′
By theorem of perpendicular axes,
IZ=IAB+IA′B′=2IAB .............(i)
Again, IZ=ICD+IC′D′=2ICD ..............(ii)
∴ From (i) and (ii),
2IAB=2ICD or IAB=ICD or I=ICD
Hence moment of inertia about CD axis= I.

Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBOOK - NCERT FINGERTIPSCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - NCERT Exemplar
8 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBOOK - NCERT FINGERTIPSCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - Assertion And Reason
15 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBOOK - NCERT FINGERTIPSCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - Rolling Motion
16 Videos
- PRACTICE PAPERSBOOK - NCERT FINGERTIPSCHAPTER - PRACTICE PAPERSEXERCISE - Practice Paper 3
50 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERT FINGERTIPSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assertion And Reason
10 Videos
Similar Questions
Knowledge Check
Let I be the moment of interia of a uniform square plate about an axis AB that passses through its centre and is parallel to two its sides. CD is a line in the plane of the plate that passes through the centre of the plate and makes an angle θ with AB. The moment of inertia of the plate about the axis CD is then equal to-
AIBIsin2θCIcos2θDIcos2(θ/2)The moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
Aincreases if its temperature is increasedBchanges if its axis of rotation is changedCincreases if its angular velocity is increasedDboth (a) and (b) are correctThe moment of inertia of a sphere of radius R about an axis passing through its centre is proportional to-
AR2BR3CR4DR5
The moment of inertia of a square plate of mass 4kg and side 1m about an axis passing through its centre and perpendicular to its plane is
View SolutionThe moment of inertia of a thin square plate ABCD of uniform thickness about an axis passing through its center and perpendicular to its plane will
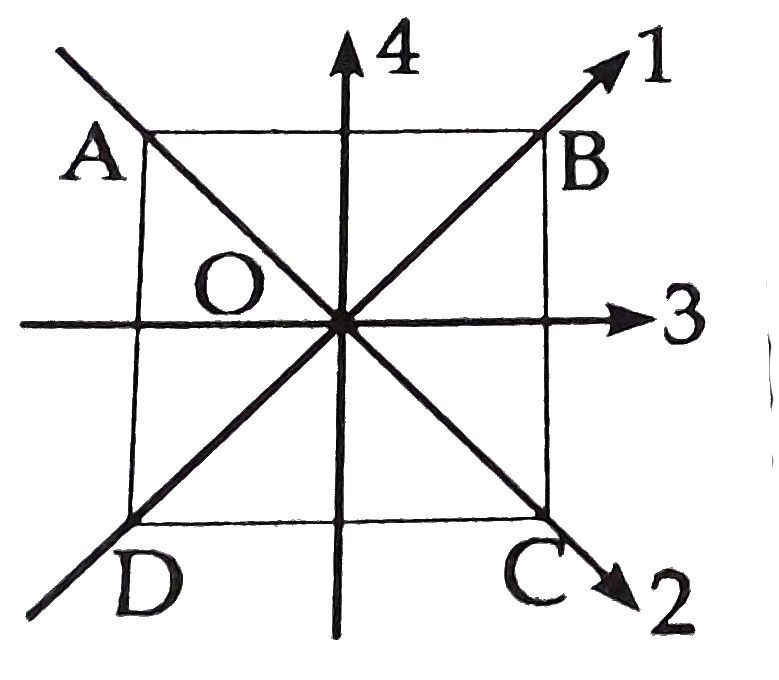
View SolutionFind moment of inertia of a uniform rectangular plate about axis zz' passing through center and perpendicular to the plane of plate, as shown in Fig.

View SolutionThe moment of inertia of a thin uniform rod of mass M, length L, about an axis passing through its centre and making an angle θ with the rod is
View SolutionThe moment of inertia of a uniform rod of length 2l and mass m about an axis xy passing through its centre and inclined at an angle α is
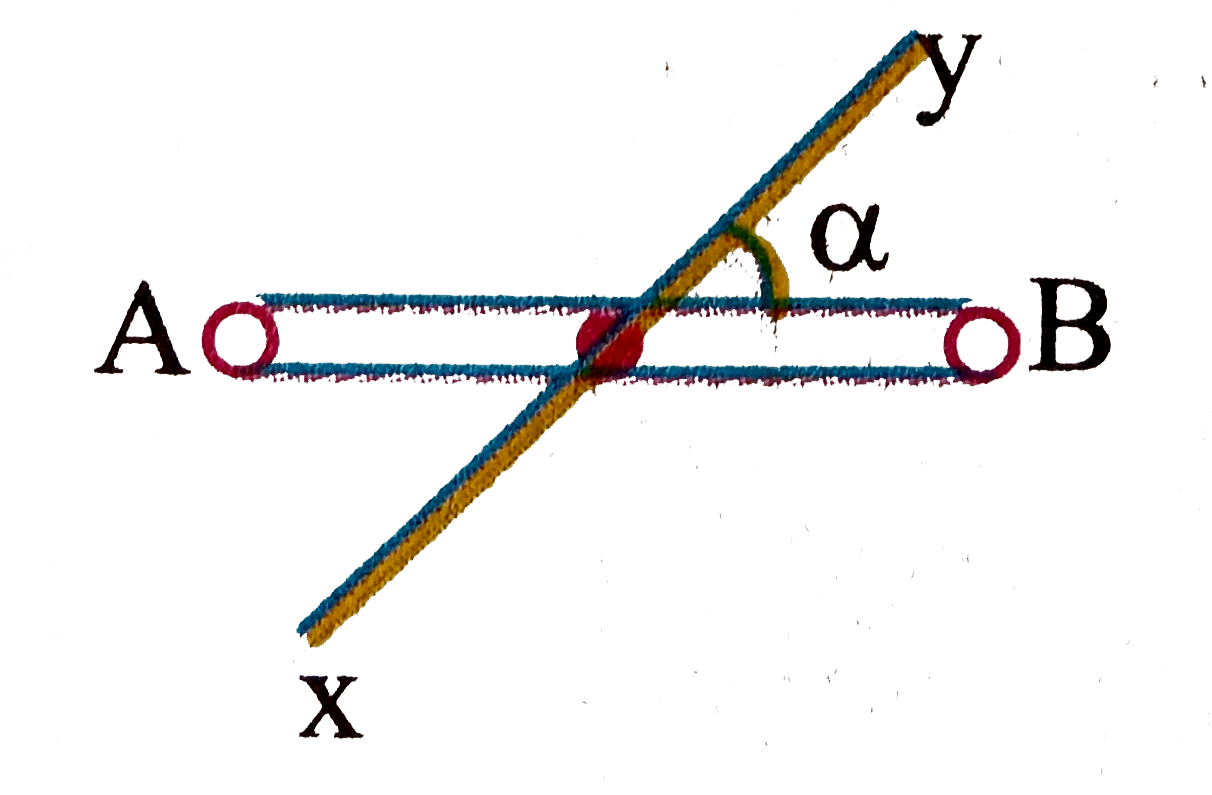
View Solution
