A rod of weight w is supported by two parallel knife edges A and B and is in equilibrium in a horizontal position. The knives are at a distance d from each other. The centre of mass of the rod is at distance x from A. The normal reaction on A is.. And on B is......

$\frac{d}{d} - x$

$d - \frac{x}{d}$

$d - \frac{x}{x}$

$\frac{x}{d} - x$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:c

Updated on:21/07/2023

A rod of weight $w$ is supported by two parallel knife edges $A$ and $B$ and is in equilibrium in a horizontal position. The knives are at a distance $d$ from each other. The centre of mass of the rod is at a distance $x$ from $A$ .
Athe normal reaction at $A$ is $\frac{w x}{d}$
Bthe normal reaction at $A$ is $\frac{w (d - x)}{d}$
Cthe normal reaction ar $B$ is $\frac{w x}{d}$
Dthe normal reaction at $B$ is $\frac{w (d - x)}{d}$ .
A uniform metre rod is bent into $L$ shape with the bent arms at $90^{\circ}$ to each other. The distance of the centre of mass from the bent point is
A $\frac{L}{4 \sqrt{2}} m$
B $\frac{L}{2 \sqrt{2}} m$
C $\frac{L}{\sqrt{2}} m$
D $\frac{L}{8 \sqrt{2}} m$
A uniform rod $A B$ hinged about a fixed point $P$ is initially vertical. A rod is released from vertical position. When rod is in horizontal position:

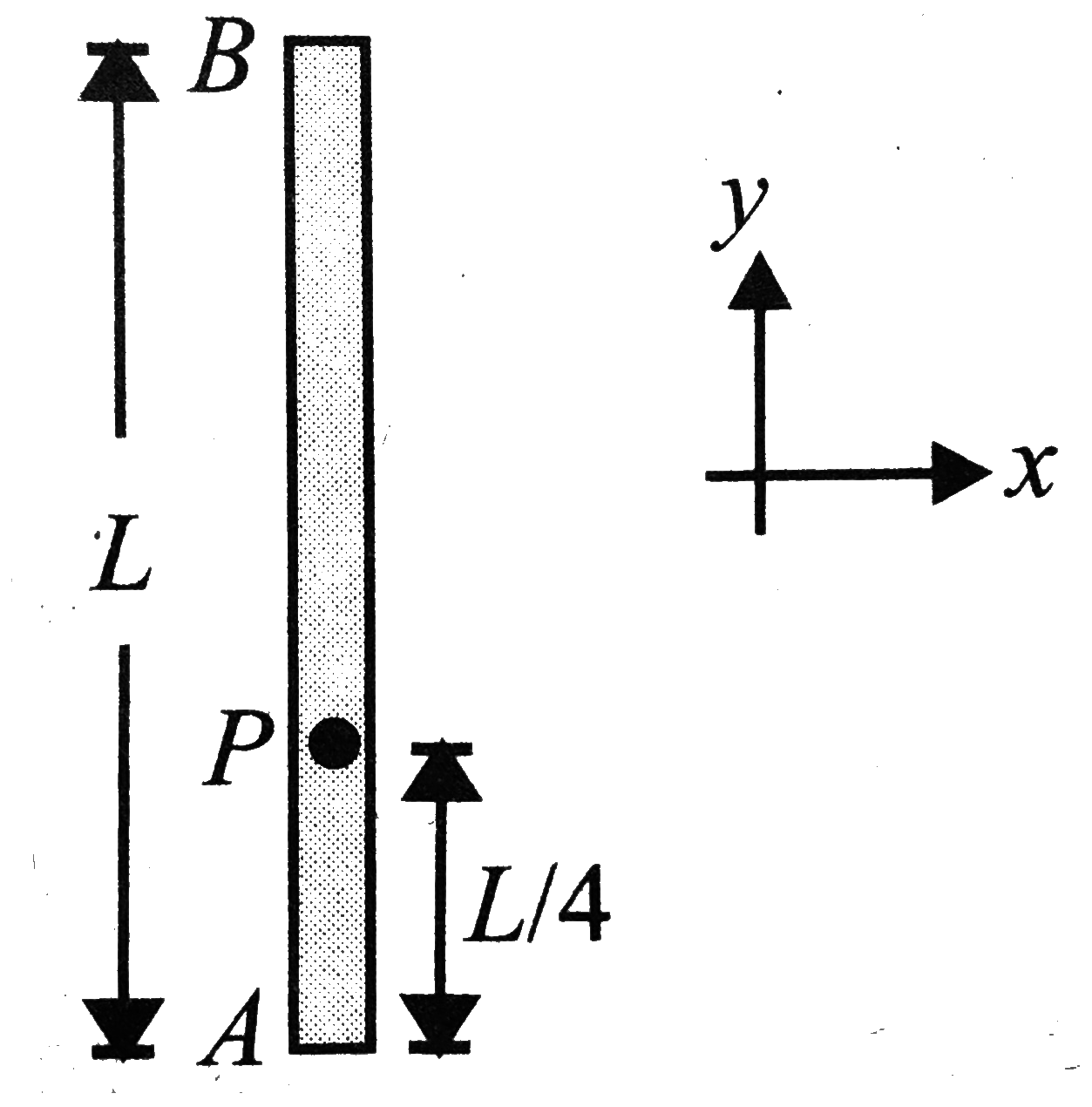
The acceleration of the centre of mass of the rod is
A $- \frac{6 g}{7} ˆ i - \frac{12 g}{7} ˆ j$
B $- \frac{12 g}{7} ˆ i - \frac{6 g}{7} ˆ j$
C $- \frac{3 g}{7} ˆ i - \frac{9 g}{7} ˆ j$
D $- \frac{9 g}{7} ˆ i - \frac{3 g}{7} ˆ j$