A particle starts from point A moves along a straight line path with an acceleration given by a=p−qx where p, q are connected and x is distance from point A . The particle stops at point B. The maximum velocity of the particle is
pq
p√q
qp
√qp
The correct Answer is:B
Given : a=p−qx
At maximum velocity, a = 0
⇒0=p−qx or x=pq
∴ Velocity is maximum at x=pq
since Acceleration,a=dvdt=dvdxdxdt=vdvdx sincev=dxdt
∴vdvdx=a=p−qx
vdv=(p−qx)dx
Integrating both sides of the above equation, we get
v22=px=(qx)22
v2=2px−qx2 or v = √2px−qx2
At x=pq,v=vmax=√2p(pq)−q(pq)2=p√q
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTIPSCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Kinematic Equations For Uniformly Accelerated Motion
32 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTIPSCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Relative Velocity
18 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTIPSCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Instantaneous Velocity And Speed
16 Videos
- MOTION IN A PLANE BOOK - NCERT FINGERTIPSCHAPTER - MOTION IN A PLANE EXERCISE - Assertion And Reason
15 Videos
- OSCILLATIONS BOOK - NCERT FINGERTIPSCHAPTER - OSCILLATIONS EXERCISE - Assertion And Reason
15 Videos
Similar Questions
A particle starts from point A, moves along a straight line path with an accleration given by a=2(4−x) where x is distance from point A. The particle stops at point B for a moment. Find the distance AB (in m). (All values are in S.I. units)
View SolutionA particle starts from point A, moves along a straight line path with an acceleration given by a=2(4−x) where x is distance from point A. The particle stops at point B for a moment. Find the distance AB(in m). (All values are in S.I. Units)
View Solution
Knowledge Check
A particle starts from rest at t=0 and moves in a straight line with an acceleration as shown below. The velocity of the particle at t=3 s is
 A5m/s2B6m/s2C10m/s2D15m/s2
A5m/s2B6m/s2C10m/s2D15m/s2A particle starting from rest moves along a straight line with constant acceleration for this velocity displacement graph will have the form-
A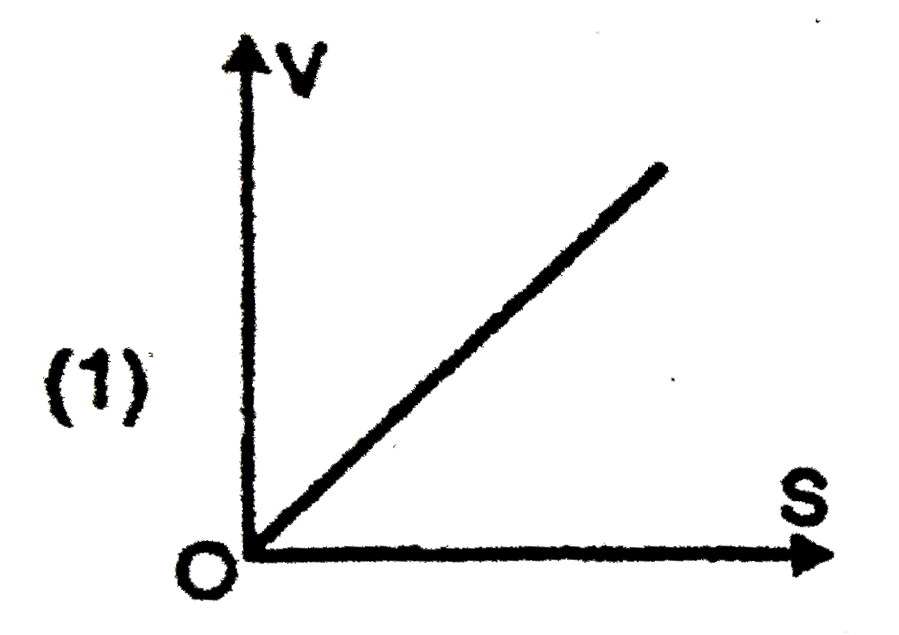 B
B C
C D
D
A particle starts from rest at t=0 and moves in a straight line with an acceleration as shown below. The velocity of the particle at t=3 s is
 A2m/sB3m/sC4m/sD6m/s
A2m/sB3m/sC4m/sD6m/s
A particle starts from rest at t=0 and moves along a straight line with a variable acceleration given by a (t)=(3t+1)ms−2 ,where t],[ is in seconds.The velocity of the particle at t=4s is
View SolutionA particle starts moving in a straight line from rest with an acceleration (inm/s2) given by : a=12√x, where x is the distance travelled by the particle (in meters ) The velocity of the particle at the instant when its acceleration is 48m/s2 is .......m/s
View SolutionA particle starts from the origin with a velocity of 2 cm/s and moves along a straight line. If the acceleration of the particle at a distance x cm from the origin be (2x−32)cms2, find the velocity of the particle at a distance 7 cm from the origin.
View Solution[" A particle starts from "],[" rest at "t=0" and moves "],[" along a straight line with "],[" a variable acceleration "],[" given by a "(t)=(3t+1)ms^(-2)],[" where "t" is in seconds."],[" The velocity of the "],[" particle at "t=4s" is "]
View SolutionA particle moves in a straight line so that its velocity at any point is given by v2=a+bx, where a,b≠0 are constants. The acceleration is
View Solution
