Two particles are projected horizontally with same speed 30m/s but in opposite directions from same height at time t=0. Calculate angle between velocity vectors of particles at time t=3s.
0∘
30∘
60∘
90∘
The correct Answer is:D
cosθ=→v1.→v2v1v2
=(30ˆi−30ˆj)30√2.(−30ˆi−30ˆj)30√2=0
⇒θ=90∘
Topper's Solved these Questions
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)32videos
TEST PAPERS
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)3videos
TEST PAPERS
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C4videos
TEST PAPERS
- BOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question32videos
SEMICONDUCTORS
Similar Questions
A particle is projected horizontally with a speed of 40√3m/s, from some height t=0. At what time its velocity makes 60∘ angle with initial velocity.
(g=10m/s2)
 View Solution
View SolutionA particle is projected at an angle of 30∘w.r.t. horizontal with speed 20m/s:( use g=10m/s2)
(i) Find the position vector of the particle after 1s.
(ii) Find the angle between velocity vector and position vector at t=1s.View Solution
Knowledge Check
- Question 1 - Select One
A particle is projected horizontally with speed 20√3m/s, from some height at t=0. At what time its velocity will make 60∘ angle with initial velocity ?
A1 secB2 secC1.5 secD2.5 sec - Question 2 - Select One
Two particles are projected with speed 4m/s and 3m/s simultaneously from same point as shown in the figure. Then :
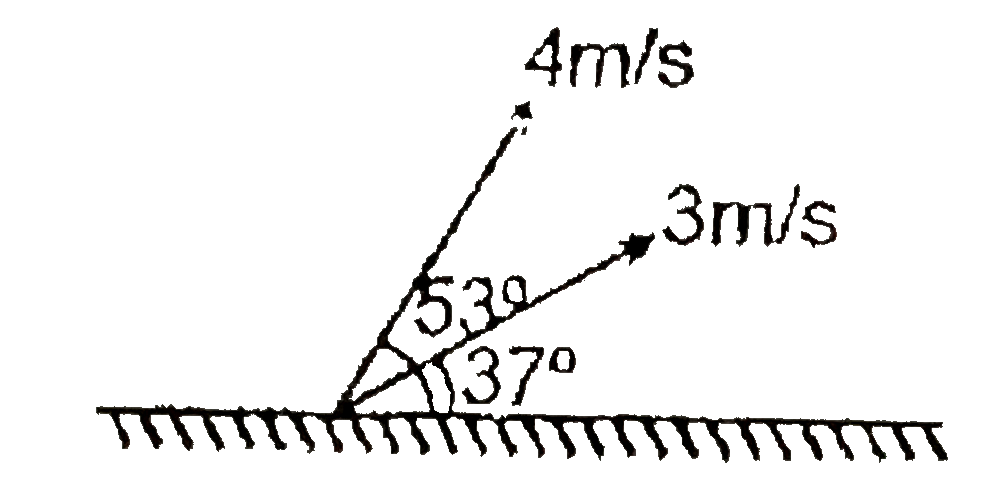 ATheir relative velocity is along horizontal direction.BTheir relative acceleration is non-zero and it is along vertical direction.CThey will hit the surface simultaneously.DTheir relative velocity is constant and has magnitude 1.4m/s
ATheir relative velocity is along horizontal direction.BTheir relative acceleration is non-zero and it is along vertical direction.CThey will hit the surface simultaneously.DTheir relative velocity is constant and has magnitude 1.4m/s - Question 3 - Select One or More
Two particles are projected with speed 4m/s and 3m/s simultaneously from same point as shown in the figure. Then:
 ATheir relative velocity is along vertical directionBTheir relative acceleration is non-zero and it is along vertical directionCThey will hit the surface simultaneouslyDTheir relative velocity is constant and has magnitude 1.4m/s
ATheir relative velocity is along vertical directionBTheir relative acceleration is non-zero and it is along vertical directionCThey will hit the surface simultaneouslyDTheir relative velocity is constant and has magnitude 1.4m/s
Two particles are projected from a tower horizontally in opposite directions with velocities 10m/sand20m/s. Find the time when their velocity vectors are mutually perpendicular. Take g=10m/s2.
View SolutionA wall OP is inclined to the horizontal ground at an angle α. Two particles are projected from points A and B on the ground with same speed (u) in directions making an angle θ to the horizontal (see figure). Distance between points A and B is x0=24m. Both particles hit the wall elastically and fall back on the ground. Time of flight (time required to hit the wall and then fall back on to the ground) for particles projected from A and B are 4 s and 2 s respectively. Both the particles strike the wall perpendicularly and at the same location. [In elastic collision, the velocity component of the particle that is perpendicular to the wall gets reversed without change in magnitude]
(a) Calculate maximum height attained by the particle projected from A.

(b) Calculate the inclination of the wall to the horizontal (α)[g=10m/s2]View SolutionA particle is projected with speed 100ms at angle θ=60∘ with the horizontal at time t=0" . At time 't' the velocity vector of the particle becomes perpendicular to the direction of velocity of projection.Its tangential acceleration at time 't' is (g=10ms2)
View SolutionTwo particles are projected simultaneously with same speed V0 in same vertical plane at angle 30∘and60∘ With the horizontal .The time at which their velocities becomes parallel is
View SolutionA particle is projected at an angle of 60∘ above the horizontal with a speed of 10m/s. After some time the direction of its velocity makes an angle of 30∘ above the horizontal. The speed of the particle at this instant is s
View Solution

