A light particle of mass m is connected to another very heavy particle by means of a light inextensible string that passes over a smooth pulley. The reading of the spring balance is approxinately
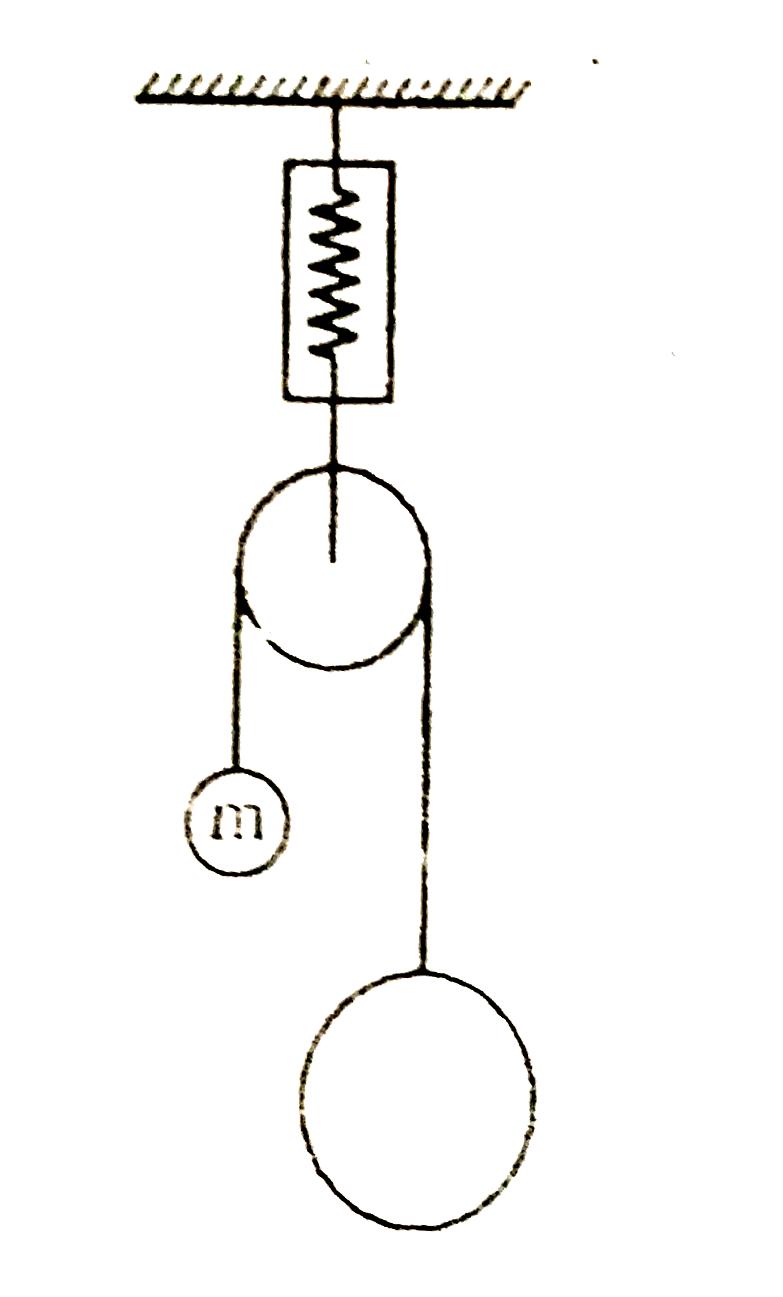
4mg
>>mg
zero
2mg
The correct Answer is:A
T=2m1m2gm1+m2
m1=m
m2= very heavy mass (M)
T=2mgm+MM
T=2mg1+mM
T≈2mg m<<M
spring balance will measure
2T=2×2mg=4mg
Topper's Solved these Questions
- TEST PAPERSBook:BANSALChapter:TEST PAPERSExercise:PHYSICS PART (A)
Explore 32 Videos
- TEST PAPERSBook:BANSALChapter:TEST PAPERSExercise:PHYSICS PART (B)
Explore 3 Videos
- TEST PAPERSBook:BANSALChapter:TEST PAPERSExercise:PHYSICS PART- C
Explore 4 Videos
- SEMICONDUCTORSBook:BANSALChapter:SEMICONDUCTORSExercise:CBSE Question
Explore 32 Videos
Similar Questions
A block of mass M is placed on a rough horizontal surface. It is connected by means of a light inextensible string passing over a smooth pulley . The other end of string is connected to a block of mass m. There is no friction between vertical surface and block m
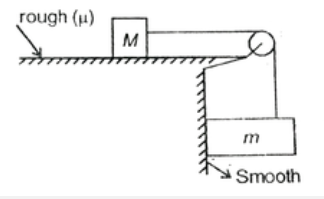
The minimum value of coefficient of friction μ such that system remains at rest , is
View SolutionA block of mass M is placed on a rough horizontal surface. It is connected by means of a light inextensible string passing over a smooth pulley . The other end of string passing over a smooth pulley. The other end of string is connected to a block of mass m. There is no friction between vertical surface and block m
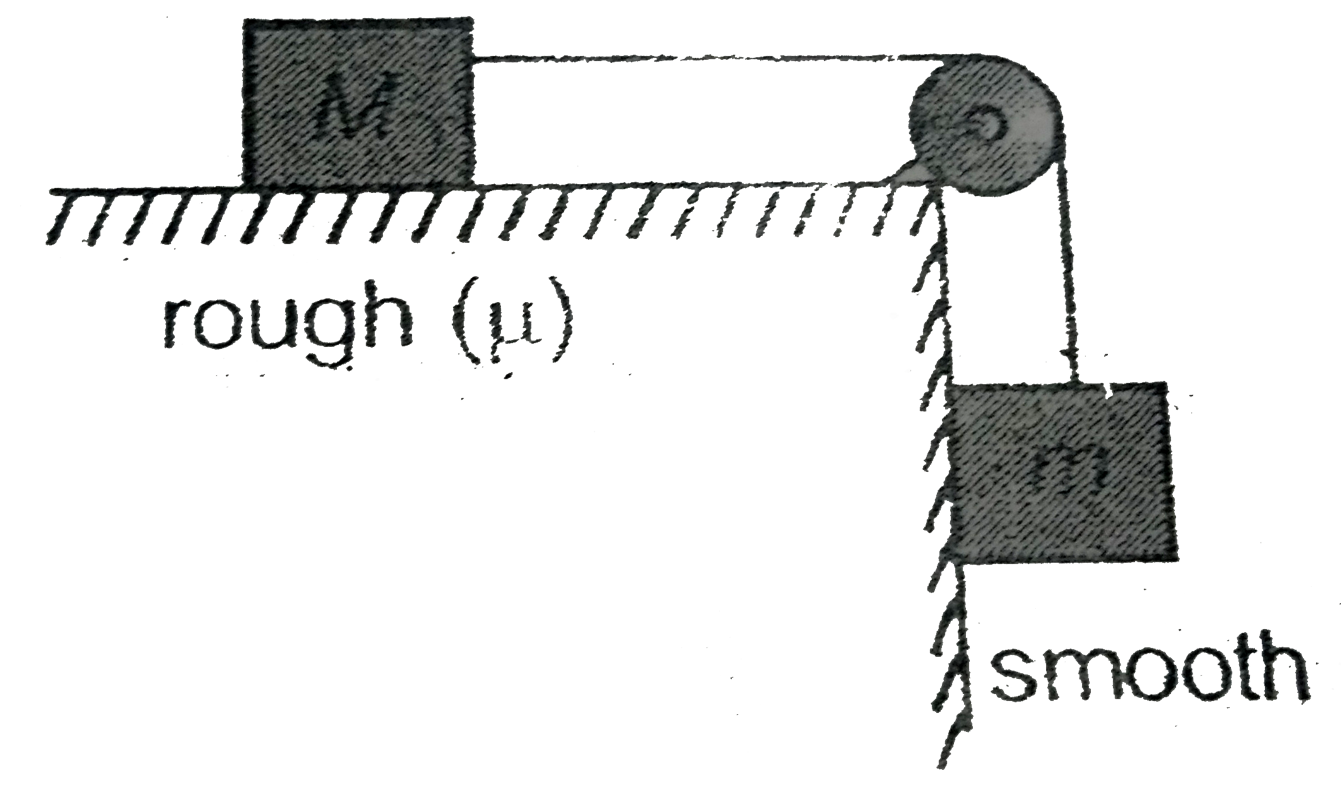
If the whole system ( horizontal surface + blocks ) accelerates towards right the value of maximum on the horizontal surface is
View Solution
Knowledge Check
A block of mass m1 lies on a smooth horizontal table and is connected to another freely hanging block of mass m2 by a light inextensible string passing over a smooth fixed pulley situated at the edge of the table. Initially the system is at rest with m1 a distance d from the pulley. Then the time taken for m1 to reach the pulley is.
 Am2gm1+m2B√2d(m1+m2)m2gC√2m2d(m1+m2)gDNone of thess
Am2gm1+m2B√2d(m1+m2)m2gC√2m2d(m1+m2)gDNone of thessTwo masses of 10 kg and 6 kg connected at the two ends of an inextensible string pass over a smooth frictionless pulley . Calculate acceleration of the system and tension in the string .
A71.5 NB72.5 NC73.5 ND74.5 NIn the figure shown, a particle of small mass m is joined to a very heavy mass M (M >> m) by a light string passing over a light pulley. The total downward force on the pulley by the string is :
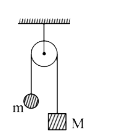 AmgB2 mgC4 mgD(M + m) g
AmgB2 mgC4 mgD(M + m) g
Two particles having mass ratio n:1 are interconnected by a light inextensible string that passes over a smooth pulley . If the system is released , then the acceleration of the centre of mass of the system is
View SolutionTwo particles A and B having equal mass are interconnected by a light inextensible string that passes over a smooth pulley. One of the amsses is pulled downward by a constant force 'F' as shown in diagram, then find the acceleration of the centre of mass of the system (A+B).
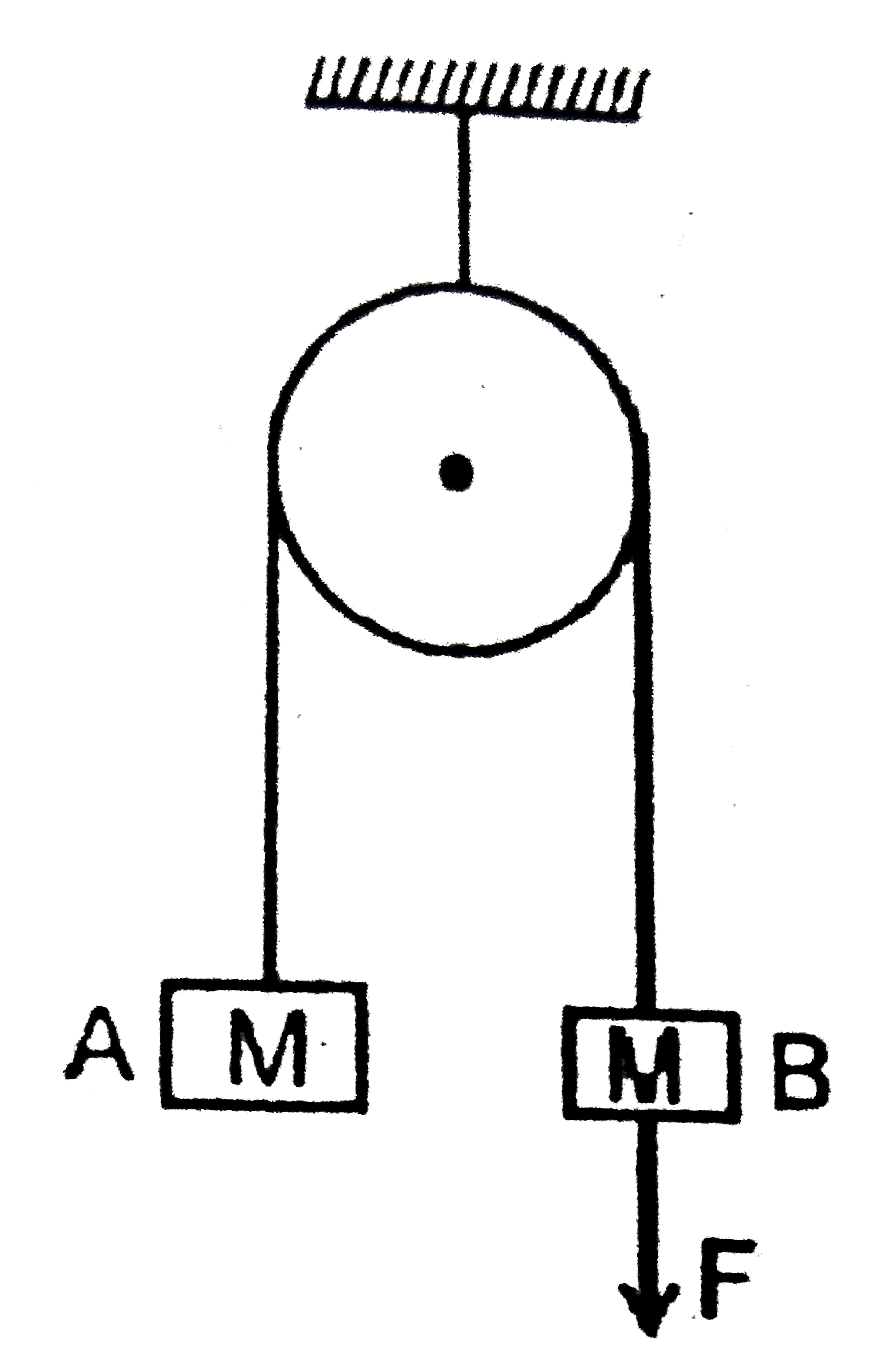
View SolutionTwo masses 8 kg and 12 kg are connected at the two ends of a light inextensible string that passes over a frictionless pulley Fibd the acceleration of the masses and tension in the string , when the masses are released
 .
.
View SolutionTwo masses M and m are connected at the two ends of an inextensible string. The string passes over a smooth frictionless pulley. Calculate the acceleration of the masses and the tension in the string. Given M>m.
View SolutionA particle of small m is joined to a very heavy body by a light string passing over a light pulley. Both bodies are free to move. The total downward force on the pulley is
View Solution
