A particle moves from A to B in a circular path of radius R covering an angle θ as shown in figure. Find the ratio of magnitude of distance and magnitude of displacement of the particle.

θ2.sinθ
θ2sin.θ2
θ2sinθ
θsin.θ2
The correct Answer is:B
Distance = Arc AB=Rθ
Displacement =2Rsin.θ2
Topper's Solved these Questions
- TEST PAPERSBook:BANSALChapter:TEST PAPERSExercise:PHYSICS PART (B)
Explore 3 Videos
- TEST PAPERSBook:BANSALChapter:TEST PAPERSExercise:PHYSICS PART (C )
Explore 15 Videos
- TEST PAPERSBook:BANSALChapter:TEST PAPERSExercise:PHYSICS
Explore 866 Videos
- SEMICONDUCTORSBook:BANSALChapter:SEMICONDUCTORSExercise:CBSE Question
Explore 32 Videos
Similar Questions
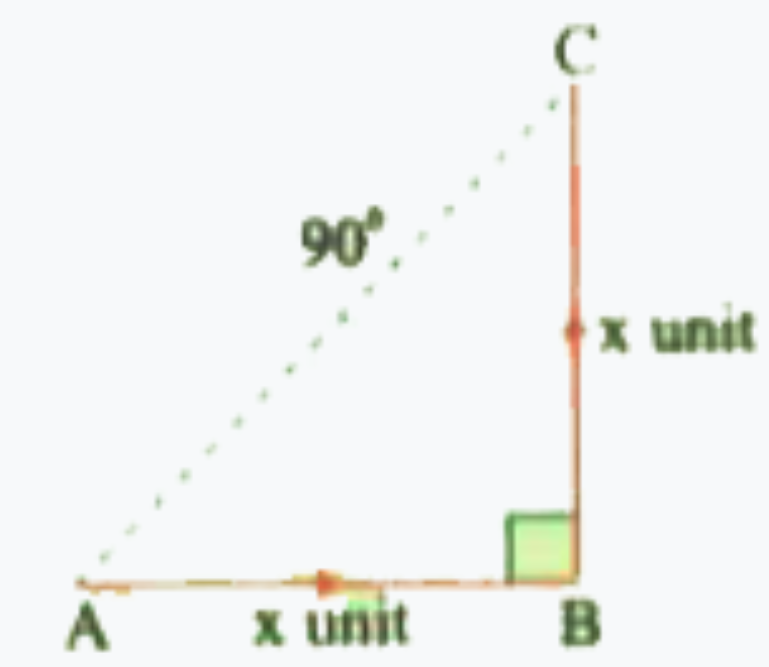
A person moves on a track ABC as shown in figure (∠B=90∘). Find distance and magnitude of displacement.
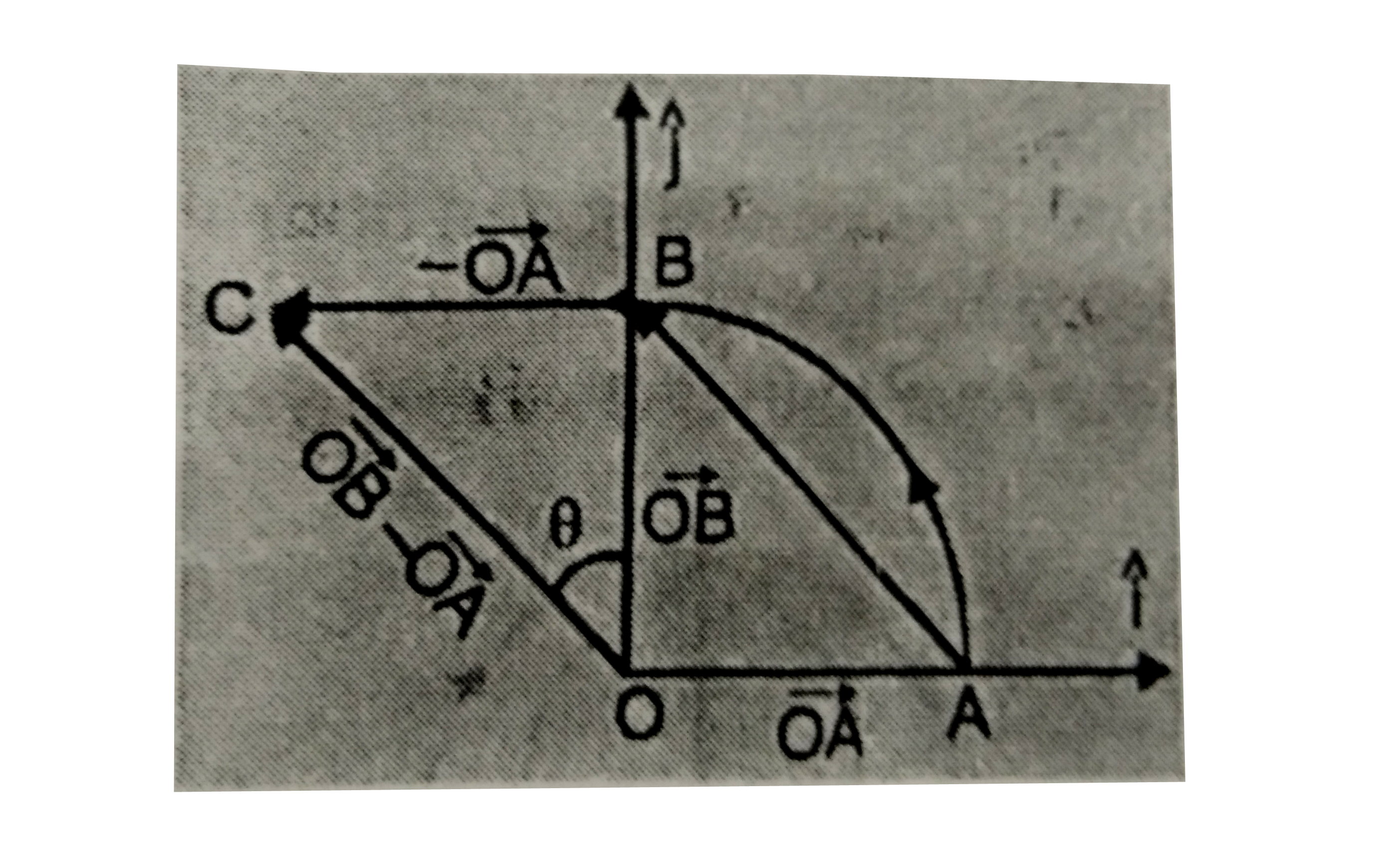
View SolutionA particle goes along a quadrant of a circle of radius 10m from A to B as shown in fig. Find the magnitude of displacement and distance along the path AB, and angle between displacement vector and x-axis ?
View Solution
Knowledge Check
A particle moves in a circular path of radius R with an angualr velocity ω=a−bt, where a and b are positive constants and t is time. The magnitude of the acceleration of the particle after time 2ab is
AaRBa2RCR(a2+b)DR√a4+b2A particle is moving uniformly in a circular path of radius r. When it moves through an angular displacement θ, then the magnitude of the corresponding linear displacement will be
A2 r cos (θ2)B2 r cot (θ2)C2 r tan (θ2)D2 r sin (θ2)A particle moves along a path ABCD as shown in the figure. Then the magnitude of net displacement of the particle from position A to D is:
 A10mB5√2mC9mD7√2m
A10mB5√2mC9mD7√2m
A particle is moving in a circular path of radius r. The displacement after half a circle would be
View SolutionA particle is moving in a circular path of radius r. The displacement after half a circle would be
View SolutionA particle is moving in a circular path of radius r. The displacement after half a circle would be
View SolutionThe path of particle is shown in figure. The ratio of distance travelled and magnitude of displacement is :
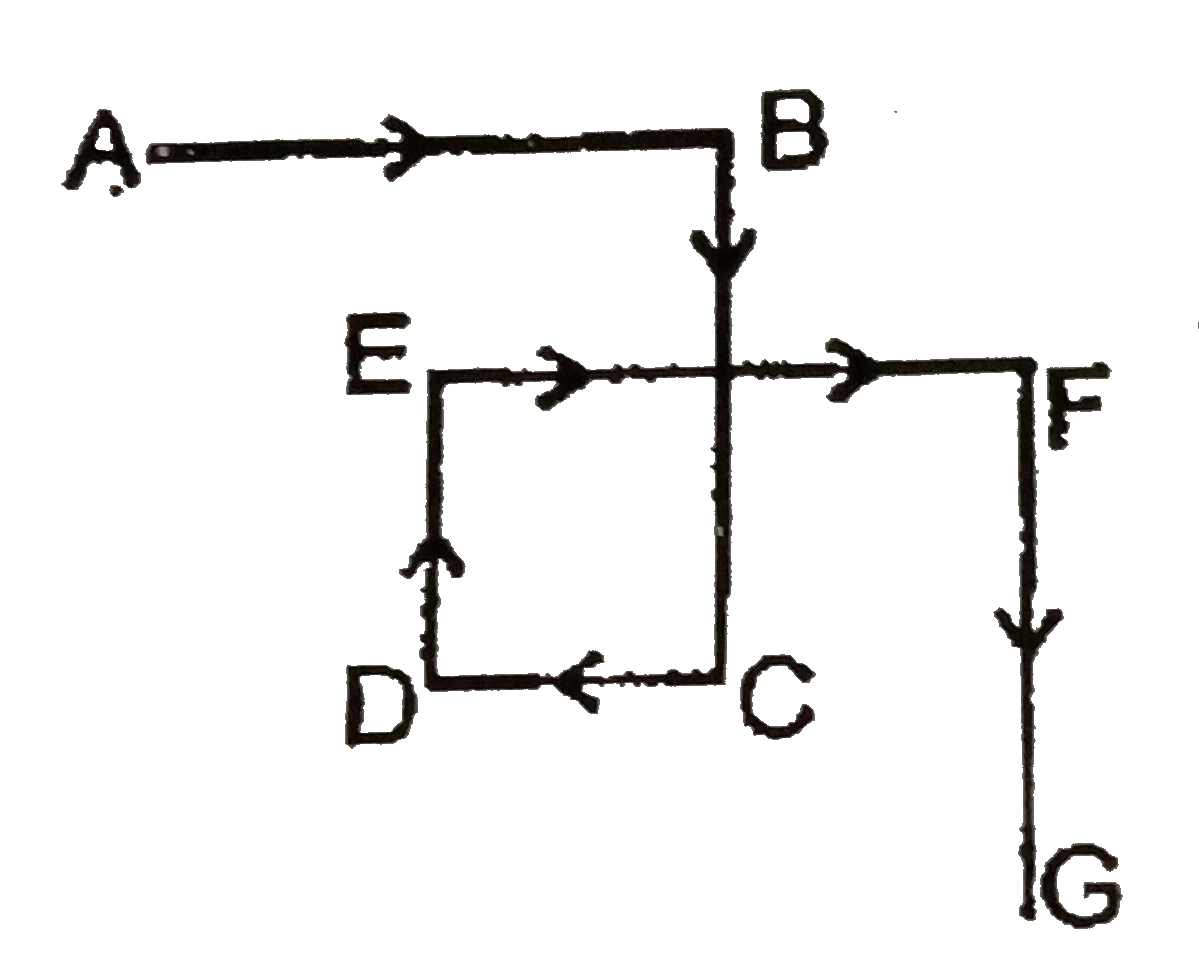
EF=AB=2m
FG =BC =2m
CD=DE =1m
View SolutionA particle moves along a circular path of radius R. The distance and displacement of a particle after one completer revolution is
View Solution

