A particle moves along x-axis. At time t=0, the particle is at origin and its initial veclocity is along positive x-direction. The plot of its (speed)2 versus its x-coordinate is as shown in graph.

The time at which velocity of particle is zero.
t=5sec
t=20sec
t=5√2sec
t=20√2sec
The correct Answer is:B
v=u+at
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)
3 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (C )
15 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS
866 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
A particle starts from rest at the origin and moves along the positive x direction. Its acceleration a versus position x graph is shown in the figure. The velocity of the particle at x = 6 m is?
View SolutionA particle starts from the origin at time t = 0 and moves along the positive x-axis. The graph of velocity with respect to time is shown in figure. What is the position of the particle at time t = 5s ?

View Solution
Knowledge Check
A particle moves along x-axis. At time t=0, the particle is at origin and its initial veclocity is along positive x-direction. The plot of its (speed)2 versus its x-coordinate is as shown in graph.

As the particle moves the acceleration of particle :Ais always uniformBdecreases with timeCincreases with timeDinformation insufficientA particle moves along x-axis. At time t=0, the particle is at origin and its initial veclocity is along positive x-direction. The plot of its (speed)2 versus its x-coordinate is as shown in graph.
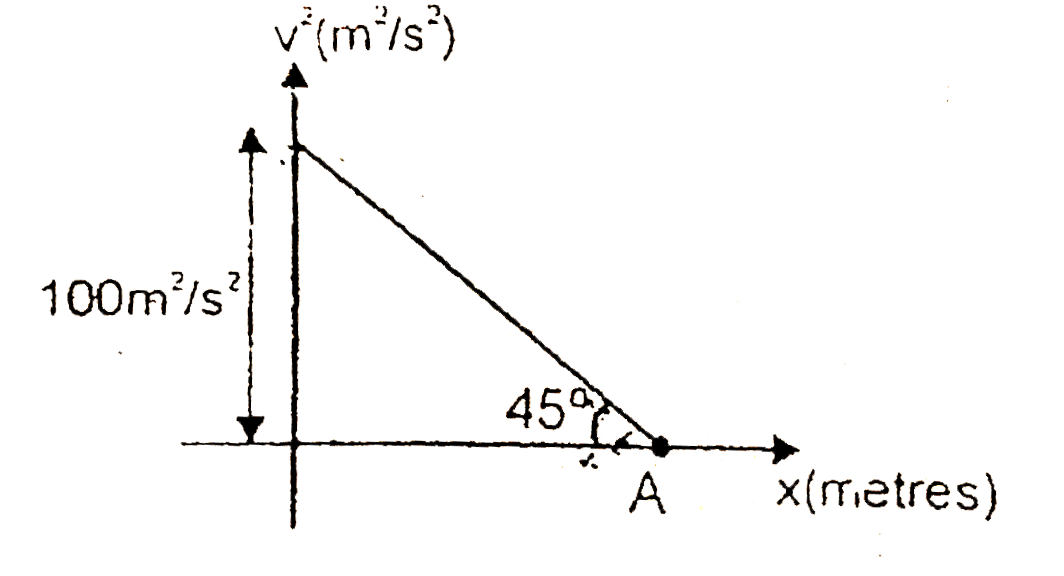
The velocity time graph for th eparticle upto point A is best represented by (assuming velocity as positive in positive x-direction):A B
B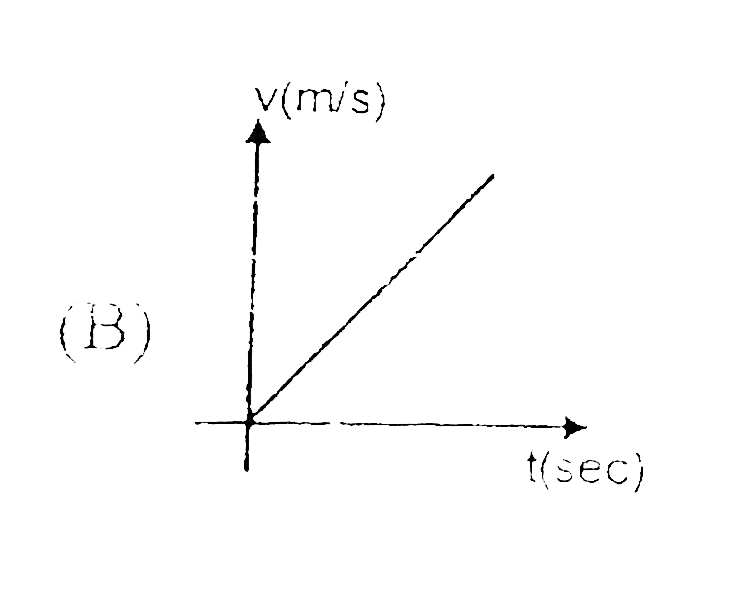 C
C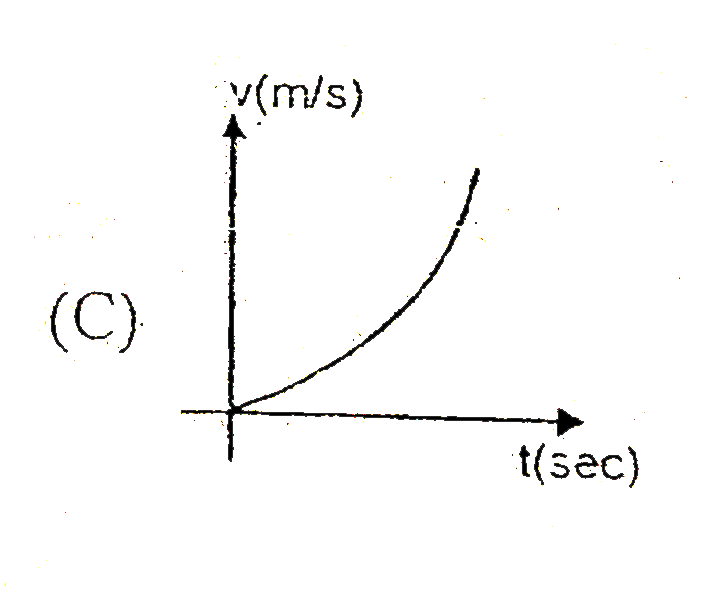 D
D
A particle is moving along X-axis Its acceleration at time t is proportional to its velocity at that time. The differential equation of the motion of the particle is
Ad2xdt2−kdxdt=0,k>0Bd2xdt2+kdxdt=0,k>0Cd2xdt2−k=0,k>0Dd2xdt2+k=0,k>0
A particle is moving along x-direction with a constant acceleration a. The particle starts from x=x0 position with initial velocity u. We can define the position of the particle with time by the relation
x=x0+ut+12at2
plot the position of the particle in relation with time is following situations
(i) If initial position of the particle is on negativ x-axis, initial velocity is positive and acceleration is negative.
(ii) If initial position is positive, initial velocity is negative and acceleration is positive.
View SolutionAcceleration of a particle moving along the x-axis is defined by the law a=−4x, where a is in m/s2 and x is in meters. At the instant t=0, the particle passes the origin with a velocity of 2m/s moving in the positive x-direction.
(a) Find its velocity v as function of its position coordinates.
(b) find its position x as function of time t.
(c) Find the maximum distance it can go away from the origin.
View SolutionA particle moves along x-axis such that its position veries with time as x=50t−5t2. Select the correct alternative (s).
View SolutionDisplacement-time equation of a particle moving along x-axis is x=20+t3−12t (SI units)
(a) Find, position and velocity of particle at time t=0.
(b) State whether the motion is uniformly accelerated or not.
(c) Find position of particle when velocity of particle is zero.
View SolutionA particle moves along x-axis in such a way that its r-coordinate varies with time't according to the equation x= (8−4t+6t2) metre. The velocity of the particle will vary with time according to the graph
View Solution
