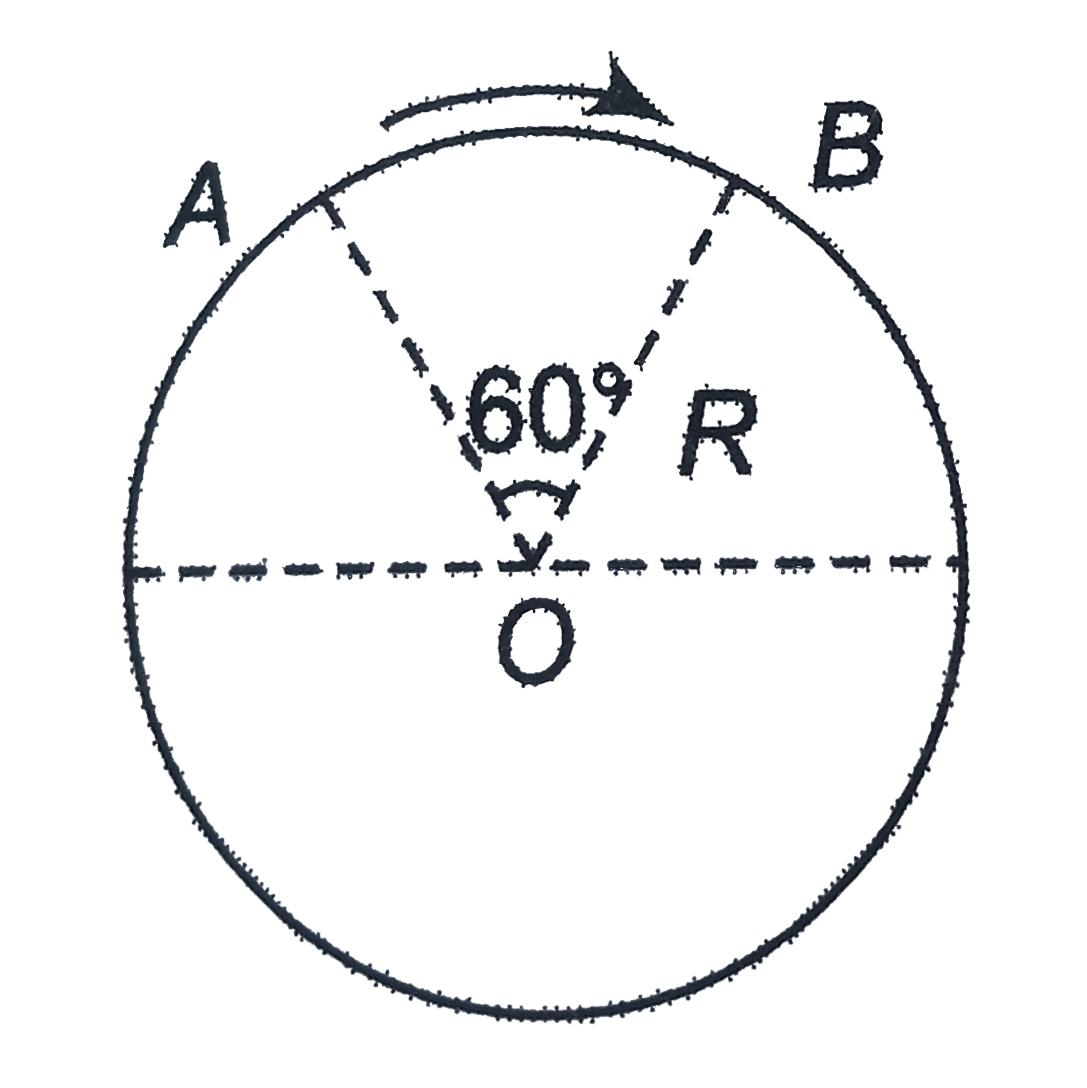
A particle goes along a quadrant of a circle of radius 10m from A to B as shown in fig. Find the magnitude of displacement and distance along the path AB, and angle between displacement vector and x-axis ?
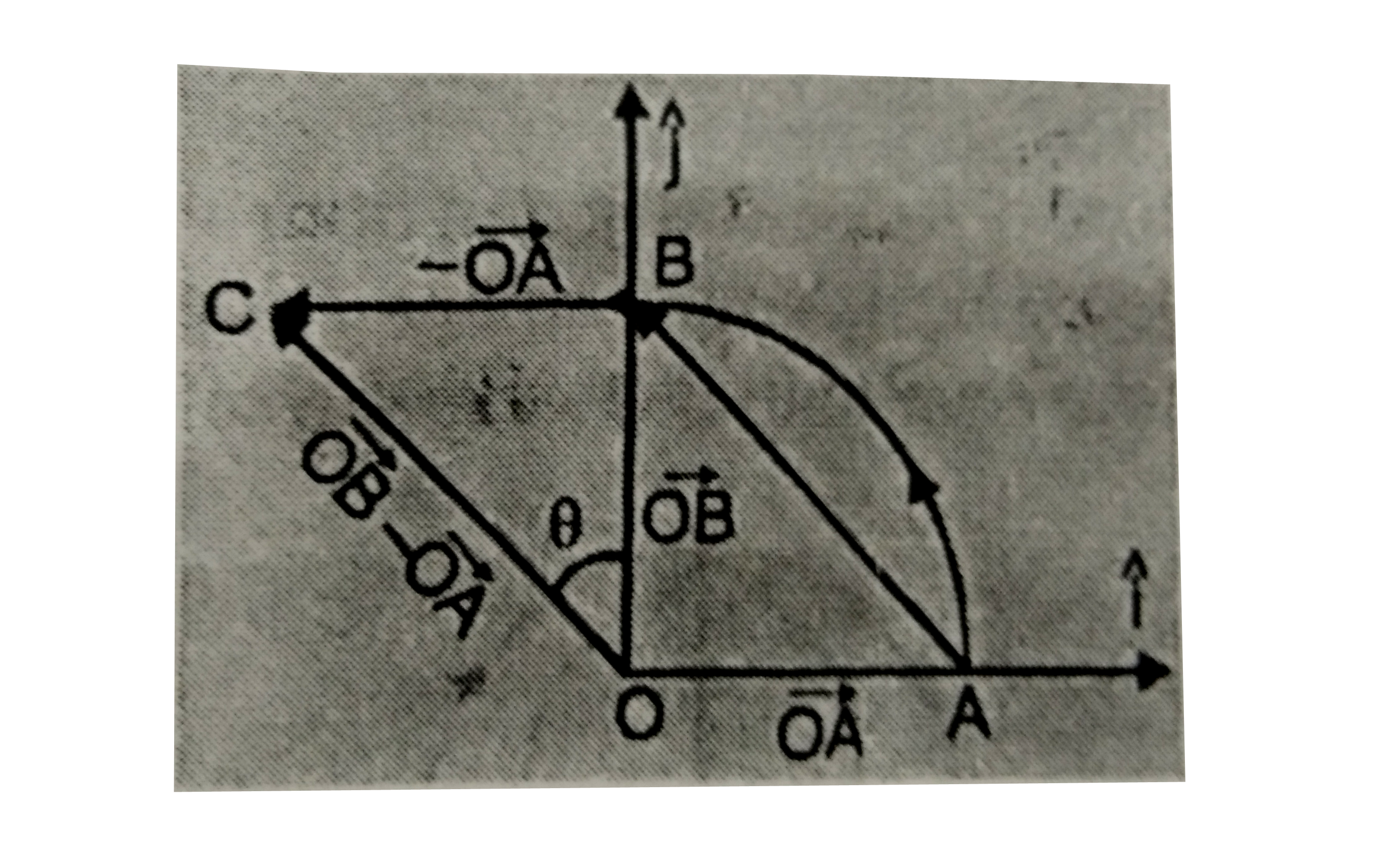
Displacement −−→AB=−−→OB−−−→OA=(10ˆj−10ˆi) m
∣∣∣−−→AB∣∣∣=√102+102=10√2m
From ΔOBCtanθ=OAOB=1010=1⇒θ=45∘
Angle between displacement vector −−→OC and x-axis = 90∘+45∘=135∘
Distance of path AB = 14 (circumference) = 14(2πR)m=(5π)m
Topper's Solved these Questions
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-1
6 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-2
7 Videos
- KINEMATICSBOOK - ALLENCHAPTER - KINEMATICSEXERCISE - Integer Type Question
3 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - SUBJECTIVE QUESTION
9 Videos
Similar Questions
Knowledge Check
A particle travels from A to B path shown in figure, then the displacement of particle is :
 .A2√2mB4√2mC52mDnone of these
.A2√2mB4√2mC52mDnone of theseA particle moves from A to B in a circular path of radius R covering an angle θ as shown in figure. Find the ratio of magnitude of distance and magnitude of displacement of the particle.
 Aθ2.sinθBθ2sin.θ2Cθ2sinθDθsin.θ2
Aθ2.sinθBθ2sin.θ2Cθ2sinθDθsin.θ2A body moves along a quadrant of a circle of radius (r). The displacement and distance traveled are.
Ar√2,πr/2Br2πrC2√2r,πrDr1πr/2
A particle moves along an arc of a circle of radius R according to the law l=asinωt, where l is the displacement from the initial position measured along the arc, and a and ω are constants. Assuming R=1.00m, a=0.80m, and ω=2.00rad/s, find:
(a) the magnitude of the total acceleration of the particle at the points l=0 and l=±a,
(b) the minimum value of the total acceleration wmin and the corresponding displacement lm.
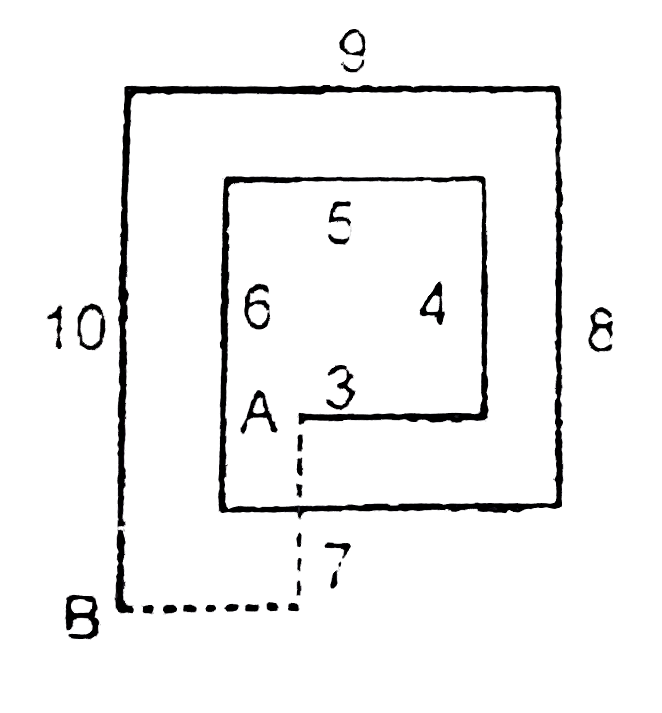
View SolutionFind the distance and displacement if the body moves from A to B along the path APQRB.
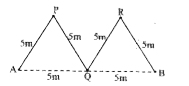
View SolutionA particle moves along a path ABCD as shown in the figure. Then the magnitude of net displacement of the particle from position A to D is:

View SolutionA particle moves along a circle of radius R with a constant angular speed ω. Its displacement (only magnitude) in time t will be
View SolutionA particle moves along a circle of radius R with a constant angular speed ω . Its displacement (only magnitude) in time t will be
View Solution