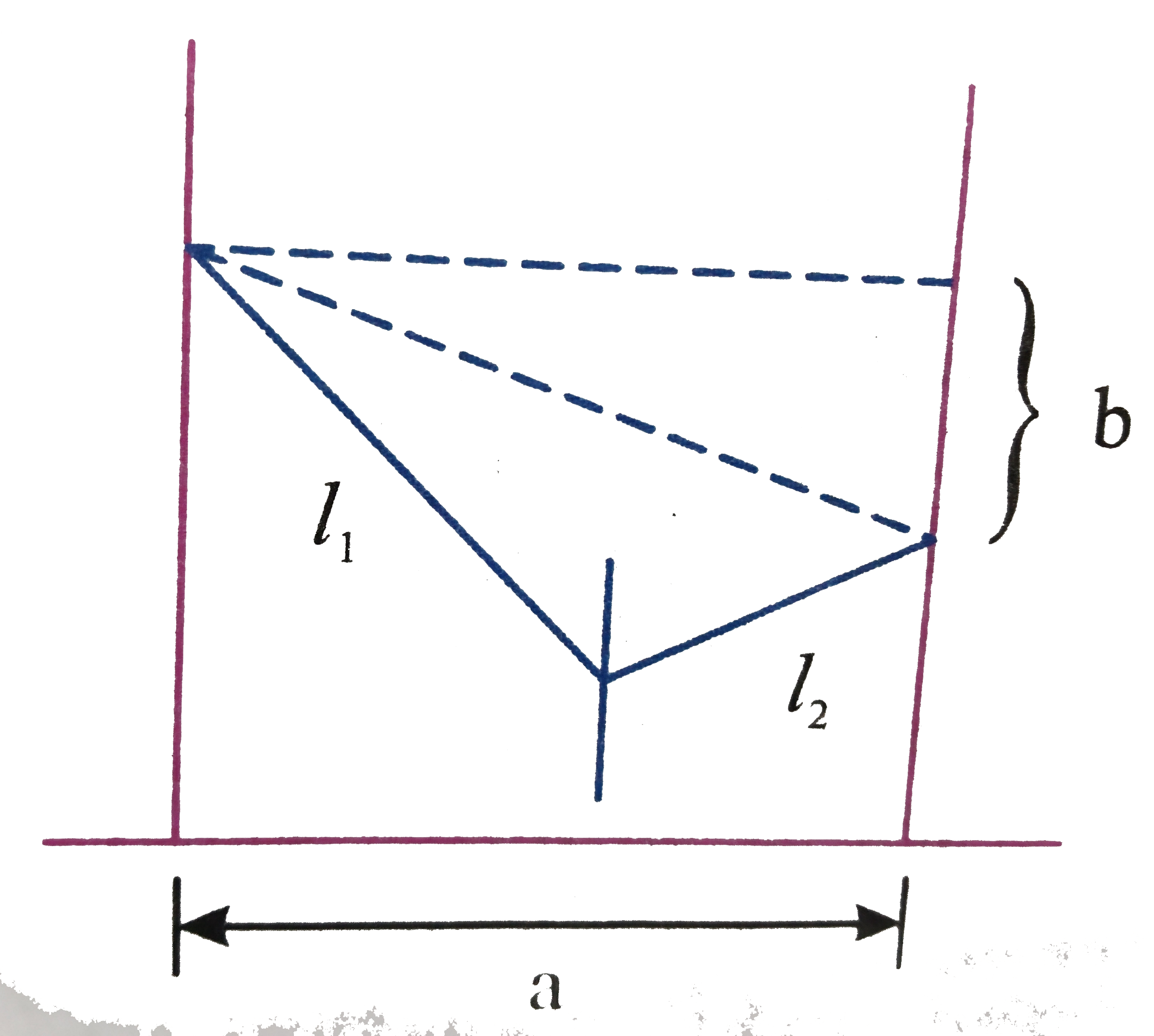
Consider a swing whose one end is fixed above the other rope by ''b'. The distance between the poles of swing is . The lengths and are such that as shown. The period of the smaller oscillations of the swing, by neglecting the height of the swinging person, is.....
The correct Answer is:A, B
Given
Let
From geometry
and
_E01_115_S01.png)
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Exercise-05(B)
Explore 46 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:MCQ s
Explore 8 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Exercise - 04[A]
Explore 25 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
Explore 25 Videos
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:PHYSICS
Explore 4 Videos
Similar Questions
One rope of a swing is fixed above the other rope by b. The distance between the poles of the swing is a. The lengths l1 and l2 of the ropes are such that l21+l22=a2+b2 (Fig ).
Determine the period T of small oscillations of the swing, neglecting the height of the swinging person in comparison with the above lengths.

View SolutionThe distance between two points P and Q is d and the lengths of projections of PQ on the coordinate planes are l1,l2,l3 then l1+l22+l23d2
View Solution
Knowledge Check
A spring has length l and force constant k it is cut into two springs of legnth l1 and l2 such that l1=nl2(n=an integer). Mass 'm' suspended form l1 oscillates with time period.
AT=2π√m(n+1)KBT=2π√nm(n+1)KCT=2π√mKDT=2π√(n+1)mKA spring has length'l' and spring constant 'k'. It is cut into two pieces of lengths l1andl2 such that l1=nl2. The force constant of the spring of length l1 is
Ak(l+n)BkCk(n+1)Dk(n+l)nA man is swinging on a swing made of 2 ropes of equal length L and in direction perpendicular to the plane of paper. The time period of the small oscillations about the mean position is
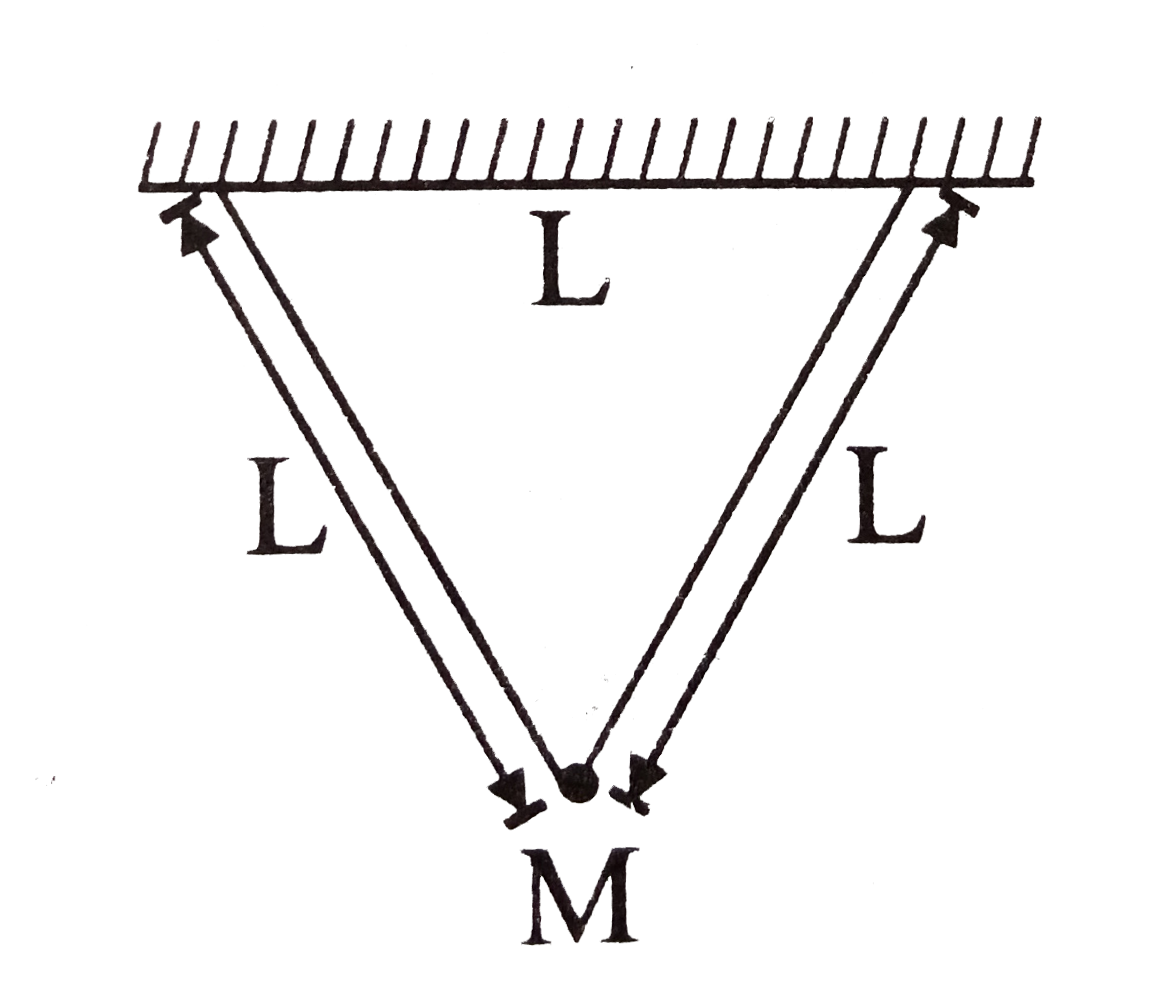 A2π√L2gB2π√√3L2gC2π√L2√3gDπ√Lg
A2π√L2gB2π√√3L2gC2π√L2√3gDπ√Lg
A compound pendulum consists of a rigid light rod having two spherical bobs of masses m1andm2 at distance l1andl2 from the centre of suspension. Find the time period of oscillations of the pendulum
View SolutionConsider the line L 1 : x 1 y 2 z 1 312 +++ ==, L2 : x2y2z3 123
View SolutionIf l1 and l2 are the lengths of a seconds pendulum at the poles and the equator of the earth, then
View SolutionIn a pipe opened at both ends n1 and n2 be the frequencies corresponding to vibrating lengths L1 and L2 respectively .The end correction is
View SolutionIn a pipe opened at both ends n1 and n2 be the frequencies corresponding to vibrating lengths L1 and L2 respectively .The end correction is
View Solution

