In the following arrangements, bock is slightly displaced vertically down from its equilibrium position and released. Find time period of vertical oscillations. The pulley is light.

If m is equilibrium tension in string must be mg and spring is stretched by h so that mg=kh. If the displace the block downward by a distance A and relesed, it starts executing SHM with amplitude A. During its ocillation we consdier the block at a displacement x below the equilibrium position, if it is moving at a speed b at this position, the pulley will be rotating at an angular speed ω given as ω=vr
_S01_025_S01.png)
Thus at this position the total energy of oscillating system is ET=12mv2+12Iω2+12k(x+h)2−mgx
Differentiating with respect to time,
we get dETdt=12m(2vdvdt)+12I(1r2)(2vdvdt)+12k[2(x+h)dxdt]−mg(dxdt)=0
or mva+Ir2va+k(x+h)v−mgv=0 or a+⎛⎜⎝km+Ir2⎞⎟⎠x=0 [as mg=kg]
comparing above equation with standard differentional equation of SHM we get ω=
⎷⎛⎜⎝km+Ir2⎞⎟⎠
Thus time period of oscillation is T=2πω=2π
⎷m+Ir2k
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Exercise-01
Explore 117 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Exercise-02
Explore 19 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
Explore 25 Videos
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:PHYSICS
Explore 4 Videos
Similar Questions
Figure shows a system consisting of a massless pulley, a spring of force constant k and ablock of mass m. If the block is slightly displaced vertically down from its equillibrium position and then released, find the period of its vertical oscillation in cases (a) & (b).
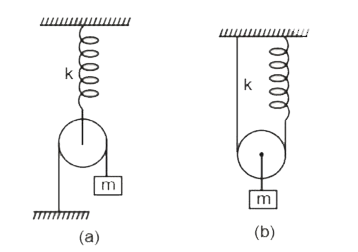
View SolutionFigure shows a system consisting of a massles pulley, a spring of force constant k and a block of mass m. If the block is sligthtly displaced vertically down from its equilibrium and released, find the period of its vertical oscillation in cases (a) and (b).

View Solution
Knowledge Check
Figure shows a system consisting of a massless pulley, a spring of force constant k and a block of mass m. If the block is slightly displaced vertically down from is equilibrium position and then released, the period of its vertical oscillation is
 A2π√mKBπ√m4KCπ√mKD4π√mK
A2π√mKBπ√m4KCπ√mKD4π√mKConsider the plane of the paper to be vertical plane with direction of 'g' as shown in the figure. A rod (MM') of mass 'M' and carrying a current I. The rod is suspended vertically through two insulated spring of spring constant K at two ends. A uniform magnetic field is applied perpendicular to the plane of the paper such that the potential energy stored in the spring, in equilibrium position is zero. If the rod is slightly displaced in the vertically direction from the position of equilibrium, then the time period of oscillation is
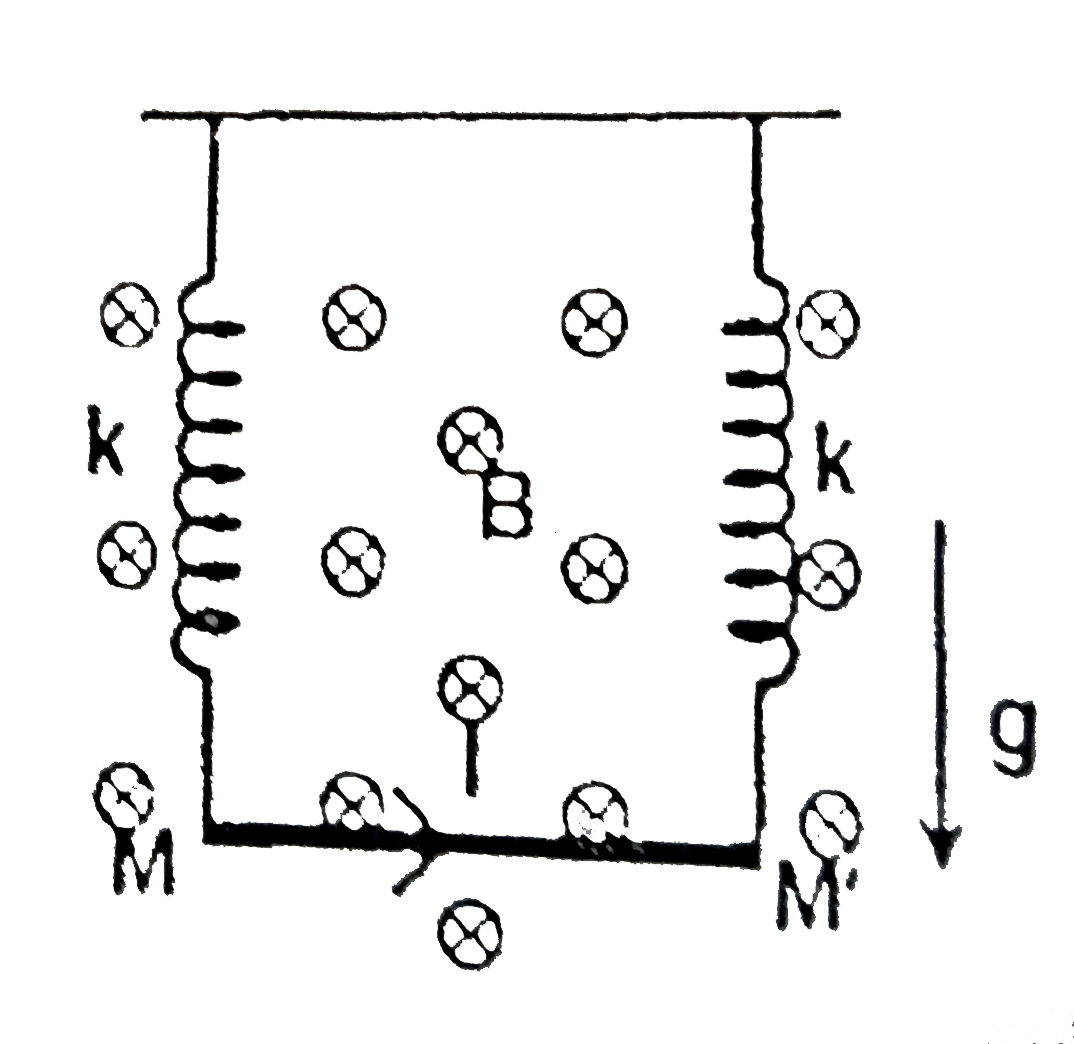 A2π√mKB2π√m2KC2π√K2mD2π√mK⋅mgIlB
A2π√mKB2π√m2KC2π√K2mD2π√mK⋅mgIlB
A system shown in the figure consists of a massless pulley, a spring of force constant k displaced vertically downwards from its equilibrium position and released, then the Period of vertical oscillations is

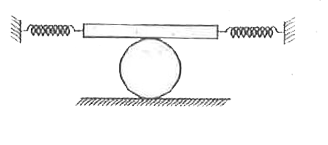
View SolutionIn the figure shown, mass of the plank is m and that of the solid cylinder is 8m. Springs are light. The plank is slightly displaced from equilibrium and then released. Find the period of small oscillations (in seconds) of the plank. There is no slipping at any contact point. The ratio of the mass of the plank adn stiffness of the spring i.e., mK=2π2
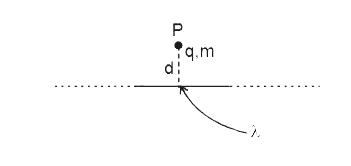
View SolutionConsider the system shown below. If the charge is slightly displaced perpendicular to the wire from its equilibrium position then find out the time period of SHM.
View SolutionA block of mass m is connected with two ideal pullies and a massless spring of spring constant K as shown in figure. The block is slightly displaced from its equilibrium position. If the time period of oscillation is μπ√mK. Then find the value of μ.

View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionA block of mass m is connected with two ideal pullies and a massless spring of spring constant K as shown in figure. The block is slightly displaced from its equilibrium position. If the time period of oscillation is μπ√mK. Then find the value of μ.

View Solution
