A light ray is incident on a transparent sphere of index = √2 , at an angle of incidence =45∘ , What is the deviation of a tiny fraction of the ray, which enters the sphere, undergoes two internal reflections and then refracts out into air?
270∘
240∘
120∘
180∘
The correct Answer is:A
To solve the problem of finding the deviation of a light ray incident on a transparent sphere with a refractive index of √2 at an angle of incidence of 45∘, we will follow these steps:
Step 1: Calculate the angle of refraction at the first interface
Using Snell's law:
n1sinθ1=n2sinθ2
where:
- n1=1 (refractive index of air)
- θ1=45∘ (angle of incidence)
- n2=√2 (refractive index of the sphere)
- θ2 is the angle of refraction.
Substituting the values:
1⋅sin(45∘)=√2⋅sin(θ2)
√22=√2⋅sin(θ2)
sin(θ2)=12⟹θ2=30∘
Step 2: Calculate the deviation at the first interface
The deviation (δ1) at the first interface is given by:
δ1=θ1−θ2=45∘−30∘=15∘
Step 3: Calculate the angles for total internal reflection (TIR)
When the light ray hits the inner surface of the sphere, it will undergo total internal reflection. The angle of incidence at the first internal reflection is 30∘.
Using the property of reflection:
Angle of reflection=Angle of incidence=30∘
Step 4: Calculate the deviation at the first TIR
The deviation (δ2) at the first TIR is given by:
δ2=180∘−2×30∘=120∘
Step 5: Calculate the angles for the second TIR
The light ray will undergo a second total internal reflection with the same angle of incidence 30∘.
Step 6: Calculate the deviation at the second TIR
The deviation (δ3) at the second TIR is also:
δ3=180∘−2×30∘=120∘
Step 7: Calculate the angle of refraction at the second interface
After the second TIR, the light ray exits the sphere. The angle of incidence at the second interface is again 30∘.
Using Snell's law again:
√2⋅sin(30∘)=1⋅sin(θ4)
√2⋅12=sin(θ4)
sin(θ4)=√22⟹θ4=45∘
Step 8: Calculate the deviation at the second interface
The deviation (δ4) at the second interface is:
δ4=θ4−θ2=45∘−30∘=15∘
Step 9: Calculate the total deviation
The total deviation (δtotal) is the sum of all deviations:
δtotal=δ1+δ2+δ3+δ4
δtotal=15∘+120∘+120∘+15∘=270∘
Thus, the total deviation of the tiny fraction of the ray is 270∘.
Using Snell's law:
n1sinθ1=n2sinθ2
where:
- n1=1 (refractive index of air)
- θ1=45∘ (angle of incidence)
- n2=√2 (refractive index of the sphere)
- θ2 is the angle of refraction.
1⋅sin(45∘)=√2⋅sin(θ2)
√22=√2⋅sin(θ2)
sin(θ2)=12⟹θ2=30∘
The deviation (δ1) at the first interface is given by:
δ1=θ1−θ2=45∘−30∘=15∘
When the light ray hits the inner surface of the sphere, it will undergo total internal reflection. The angle of incidence at the first internal reflection is 30∘.
Angle of reflection=Angle of incidence=30∘
The deviation (δ2) at the first TIR is given by:
δ2=180∘−2×30∘=120∘
The light ray will undergo a second total internal reflection with the same angle of incidence 30∘.
The deviation (δ3) at the second TIR is also:
δ3=180∘−2×30∘=120∘
After the second TIR, the light ray exits the sphere. The angle of incidence at the second interface is again 30∘.
√2⋅sin(30∘)=1⋅sin(θ4)
√2⋅12=sin(θ4)
sin(θ4)=√22⟹θ4=45∘
The deviation (δ4) at the second interface is:
δ4=θ4−θ2=45∘−30∘=15∘
The total deviation (δtotal) is the sum of all deviations:
δtotal=δ1+δ2+δ3+δ4
δtotal=15∘+120∘+120∘+15∘=270∘
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE-2
44 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE-3
12 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 05 (B) (ASSERTION & REASON )
9 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
427 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
A light ray is incident on a transparent sphere of index = √2 , at an angle of incidence =45∘ , What is the deviation of a tiny fraction of the ray, which enters the sphere, undergoes two internal reflections and then refracts out into air?
View SolutionA light ray is incident on a glass sphere at an angle of incidence 60∘ as shown. Find the angles r, r', e and the total deviation after two refractions.

View Solution
Knowledge Check
A ray of light is incident on a medium of refractive index √2 at an angle of incidence of 45∘. The ratio of the width of the incident beam in air to that of the refracted beam in the medium is
A(3/2)1/2B(2/3)1/2C3/2D2/3A ray of light strikes a transparent rectangular slab of refractive index √2 at an angle of incidence of 45∘. The angle betweent the reflected and refracted rays is
A75∘B90∘C105∘D120∘A ray of light strikes a transparent rectangular slab of refractive index √2 at an angle of incidence of 45∘. The angle between the reflected and refracted rays is
A75∘B90∘C105∘D120∘
A light ray is incident on a glass sphere at an angle of incidence 60∘ as shown. Find the angles r,f1,e and the total deviation after two refractions.

View SolutionA light ray is incident on a glass sphere of reflective index μ=√3 at an angle of incidence 60∘ as shown in Fig. Find the angles r, r′ e and the total deviation after two refractions.
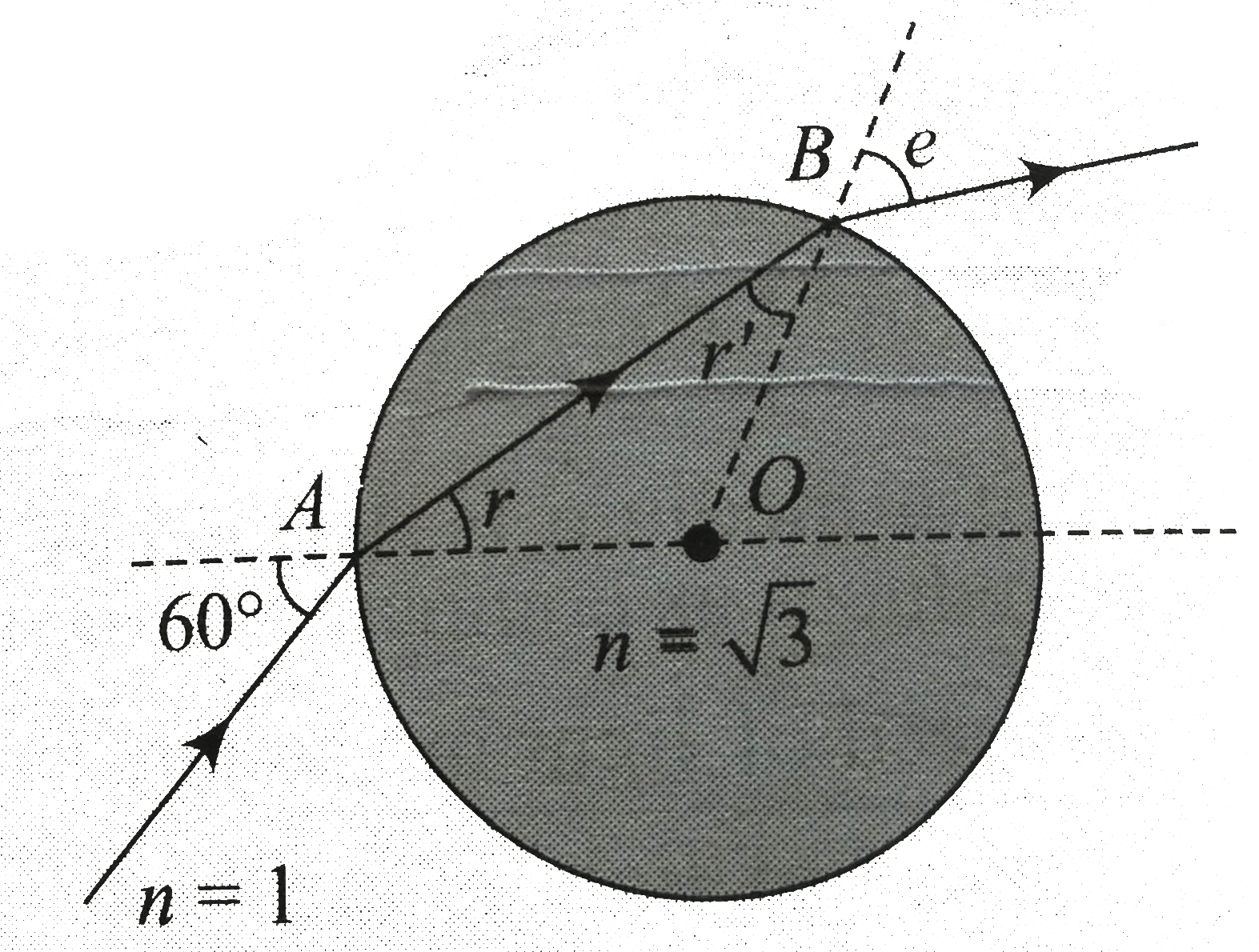
View SolutionA ray of light is incident on a transparent plate of a material of refractive index √3 at the polarising angle. Find the angle of refraction.
View SolutionA ray of light is incident on the surface of water. For what angle, the ray will undergo total internal reflection ?
View SolutionA ray of light incident on a transparent block at an angle of incident 60∘. If the refractive index of the block is 1.732, the angle of deviation of the refracted ray is
View Solution
