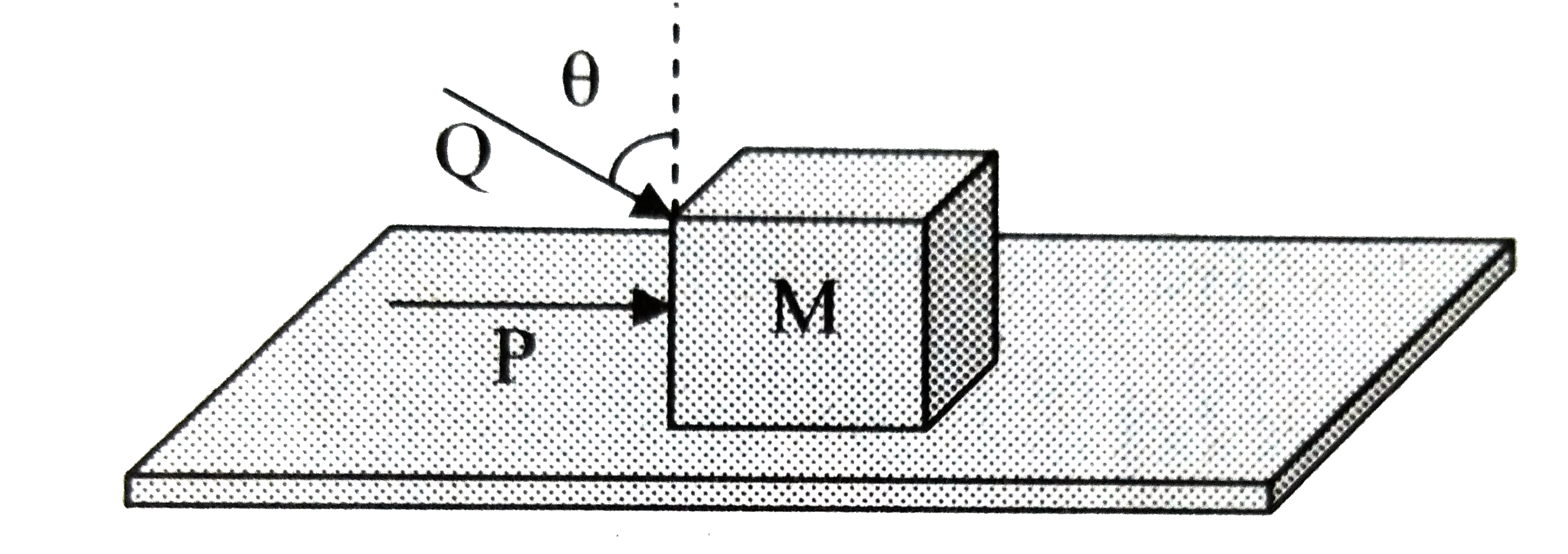
A block of mass m lying on a rough horizontal plane is acted upon by a horizontal force P and another force Q inclined at an angle θ to the vertical. The minimum value of coefficient of friction of friction between the block and the surface for which the block will remain in equilibrium is

P+Qsinθmg+Qcosθ
Pcosθ+Qmg−Qsinθ
P+Qcosθmg+Qsinθ
Ψnθ+Qmg−Qcosθ
The correct Answer is:A
Qcosθ+mg=N
P+Qsinθ=μN
∴μ=P+QsinθQcosθ+mg
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-III
Explore 28 Videos
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-I
Explore 52 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBook:ALLENChapter:NEWTON'S LAWS OF MOTION & FRICTIONExercise:EXERCISE (JA)
Explore 4 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
Explore 25 Videos
Similar Questions
A block of mass m lying on a rough horizontal plance is acted upon by a horizontal force P and another force Q inclined at an angle θ to the vertical. The block will remain in equilibrium, if the coefficient of friction between it and the surface is
View SolutionA block of mass 4kg rests on a rough horizontal plane. The plane is gradually inclined until at an angle θ=60∘ , with the vertical, the mass just begins to side. What is the coefficient of static friction between the block and the plane?
View Solution
Knowledge Check
A block of mass m lying on a rough horizontal plance is acted upon by a horizontal force P and another force Q inclined at an angle θ to the vertical. The block will remain in equilibrium, if the coefficient of friction between it and the surface is
 AP+Qsinθmg+QcosθBPcosθ+Qmg−QsinθCP+Qcosθmg+QsinθDPsinθ+Qmg−Qcosθ
AP+Qsinθmg+QcosθBPcosθ+Qmg−QsinθCP+Qcosθmg+QsinθDPsinθ+Qmg−QcosθA block of mass m lying on a horizontal plane , is acted upon by a horizontal force p and another force Q inclined at an angle θ to the vertical .The block will remain in equilibrium if the coefficient of friction between it and the surface is (assume p>Q)
 A(Psinθ−Q)/(mg−cosθ)B(P−Qsinθ)/(mg+cosθ)C(Pcosθ+Q)/(mg−cosθ)D(P+Qsinθ)/(mg+Qcosθ)
A(Psinθ−Q)/(mg−cosθ)B(P−Qsinθ)/(mg+cosθ)C(Pcosθ+Q)/(mg−cosθ)D(P+Qsinθ)/(mg+Qcosθ)
A wedge of mass m, lying on a rough horizontal plane, is acted upon by a horizontal force F1 and another force F2, inclined at an angle θ to the vertical. The block is in equilibrium, then minimum coefficient of friction between it and te surface isA(F2sinθ)/(mg+F2cosθ)B(F1cosθ+F2)/(mg−F2sinθ)C(F1+F2sinθ)/(mg+F2cosθ)D(F2sinθ−F2)/(mg−F2cosθ)
A block of weight 200N is pulled along a rough horizontal surface at constant speed by a force of 100N acting at an angle 30∘ above the horizontal. The coefficient of kinetic friction between the block and the surface is
View SolutionA block of weight 200N is pulled along a rough horizontal surface at contant speed by a force of 100N acting at an angle 30∘ above the horizontal. The coefficient of kinetic friction between the block and the surface is .
View SolutionA wooden block of mass M resting on a rough horizontal surface is pulled with a force F at an angle with the horizontal. If is the coefficient of kinetic friction between the block and the surface, then acceleration of the block is -
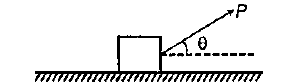
View SolutionA block of weight w rests on a horizontal plane. A force P inclined at an angle theta to the plane is applied to the block until it is on the of motion. Find the value of coefficient of friction.
View SolutionA block of mass m is lying on horizontal surface of coefficient of friction μ. A force is applied to the block at an angle θ with the horizontal. The block will move with a minimum force F if
View Solution

