A frame will be inertial, if it moves with respect to another inertial frame with a constant :-
Linear velocity
Angular velocity
Linear acceleration
All of the above
The correct Answer is:A
Step by step video, text & image solution for A frame will be inertial, if it moves with respect to another inertial frame with a constant :- by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-III
Explore 28 Videos
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-I
Explore 52 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBook:ALLENChapter:NEWTON'S LAWS OF MOTION & FRICTIONExercise:EXERCISE (JA)
Explore 4 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
Explore 25 Videos
Similar Questions
Knowledge Check
Statement I: A concept of pseudo force is valid both for inertial as well as non-inertial frame of reference.
Statement II: A frame accelerated with respect to an inertial frame is a non-inertial frame.AStatement I is true, statement II is true, Statement II is the correct explanation for statement I.BStatemet I is true, Statement II is true , Statement II is NOT the correct explanation for Statement ICStatement I is True, Statement II is False.DStatement I is False, Statement II is trueA frame of reference A is moving rectilinearly and uniformly with a velocity →u with respect to an inertial frame B. A body is moving with velocity →v and acceleration →a in an inertial system.
(A): When we use Newton's second law in frame B we write Σ→Fnet=m→a Now, when we use the same in frame A we will write exactly same →Fnetand→a
(R): All inertial systems are equally suitable for the description of physical phenomenon.AIf both A and R are true and R is the correct explanation of ABIf both A and R are true but R is not correct explanation of ACIf A is true but R is falseDIf A is false but R is trueA frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity ω is an example of non=inertial frame of reference. The relationship between the force →Frot experienced by a particle of mass m moving on the rotating disc and the force →F∈ experienced by the particle in an inertial frame of reference is
→Frot=→Fin+2m(→vrot×→ω)+m(→ω×→r)×→ω.
where →vrot is the velocity of the particle in the rotating frame of reference and →r is the position vector of the particle with respect to the centre of the disc.
Now consider a smooth slot along a diameter fo a disc of radius R rotating counter-clockwise with a constant angular speed ω about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis (→ω=ωˆk). A small block of mass m is gently placed in the slot at →r(R/2)ˆi at t=0 and is constrained to move only along the slot.
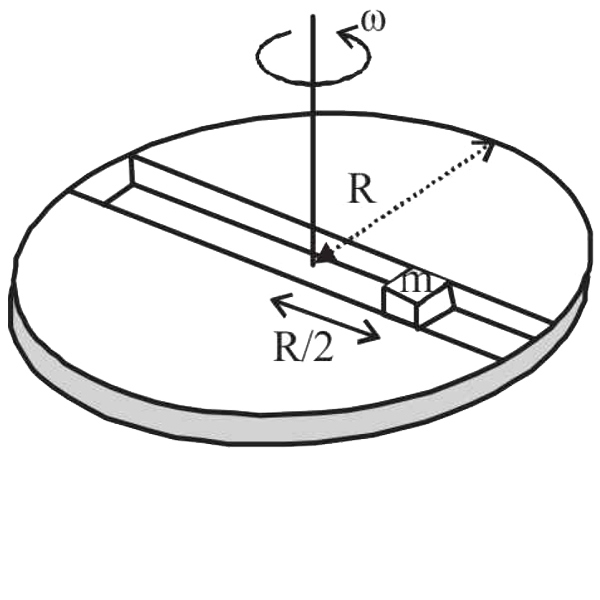
The distance r of the block at time isA(a) R4(eωt+e−ωt)B(b) R2cosωtC(c) R4(e2ωt+e−2ωt)D(d) R2cos2ωt
Consider a rocket that is in deep space and at rest relative to an inertial reference frame. The rocket's engine is to be fired for a certain interval. What must be the rocket's mass ratio (ratio of initial to final mass) over that interval if the rocket's original speed relative to the inertial frame is to be equal to (a) the exhaust speed (speed of the exhaust products relative to the rocket) and (b) 2.0 times the exhaust speed?
View SolutionA frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity ω is an example of non=inertial frame of reference. The relationship between the force →Frot experienced by a particle of mass m moving on the rotating disc and the force →F∈ experienced by the particle in an inertial frame of reference is
→Frot=→Fin+2m(→vrot×→ω)+m(→ω×→r)×→ω.
where →vrot is the velocity of the particle in the rotating frame of reference and →r is the position vector of the particle with respect to the centre of the disc.
Now consider a smooth slot along a diameter fo a disc of radius R rotating counter-clockwise with a constant angular speed ω about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis (→ω=ωˆk). A small block of mass m is gently placed in the slot at →r(R/2)ˆi at t=0 and is constrained to move only along the slot.
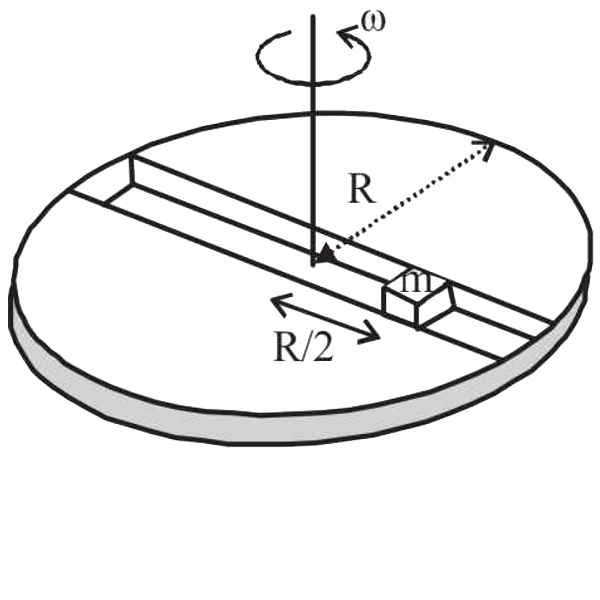
The net reaction of the disc on the block is
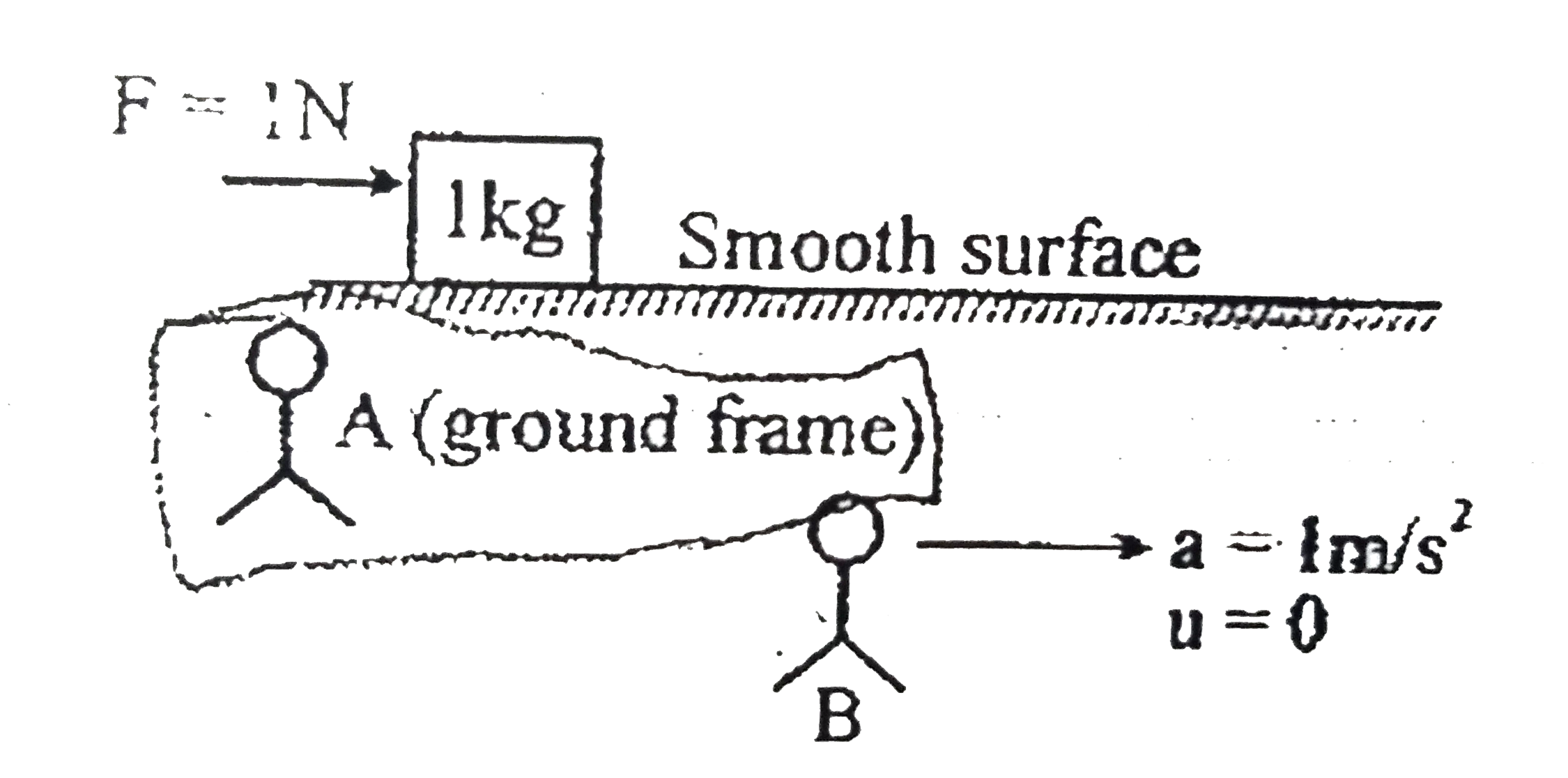
View SolutionAn observer A is at rest in gournd frame, observer B is moving with constant another observer C is moving with constant velocity of 1m/s.
View SolutionStatement I: A particle is found to be a rest when seen from a frame S1 and moving with a constant velocity when seen from another frame S2. We can say both the frames are inertial.
Statement II: All frames moving uniformly with respect to an inertial frame are themselves inertial.
View SolutionA frame of reference F2 moves with velocity →v with respect to another frame F1. When an object is observed from both frames, its velocity is found to be →v1 in F1 and →v2 is equal to
View Solution

