What force F must be applied so that m1 and m2 are at rest on m3 in
(m1+m2+m3)m2gm1
(m1+m2)m2gm1
(m2+m3)m1gm2
(m1+m3)m1gm2
The correct Answer is:A
a=F(m1+m2+m3)
T=m2g=m1×F(m1+m2+m3)
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-III
Explore 28 Videos
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-I
Explore 52 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBook:ALLENChapter:NEWTON'S LAWS OF MOTION & FRICTIONExercise:EXERCISE (JA)
Explore 4 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
Explore 25 Videos
Similar Questions
In the adjoining figure all surface are frictionless . What force F must by applied to M1 to keep M3 free from rising or falling?

View SolutionIn the figure2.217 all the surfaces are frictionless. What force F is required to be applied on the bigger block so that m2 and m3 will remain at rest on it.
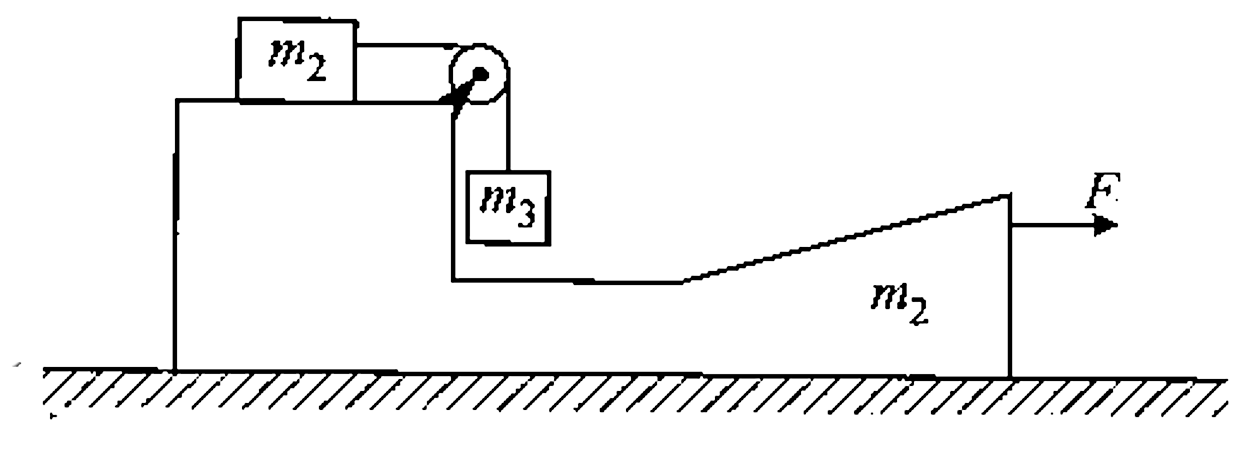
View Solution
Knowledge Check
All surfaces assumed to be frictionless calculate the horizontal force F that must be applied so that m1 and m2 do not move relative to m3 is :–
 A(m1+m2+m3)m2gm1B(m1+m2)m2gm1C(m2+m3)m1gm2D(m1+m3)m1gm2
A(m1+m2+m3)m2gm1B(m1+m2)m2gm1C(m2+m3)m1gm2D(m1+m3)m1gm2A large cubical shaped block of mass M rests on a fixed horizontal surface. Two blocks of mass m1 and m2 are connected by a light inextensible string passing over a light pulley as shown. Neglect friction everywhere. Then the constant horizontal force of magnitude F that should be applied to M so that m1 and m2 do not mov relative toM is:
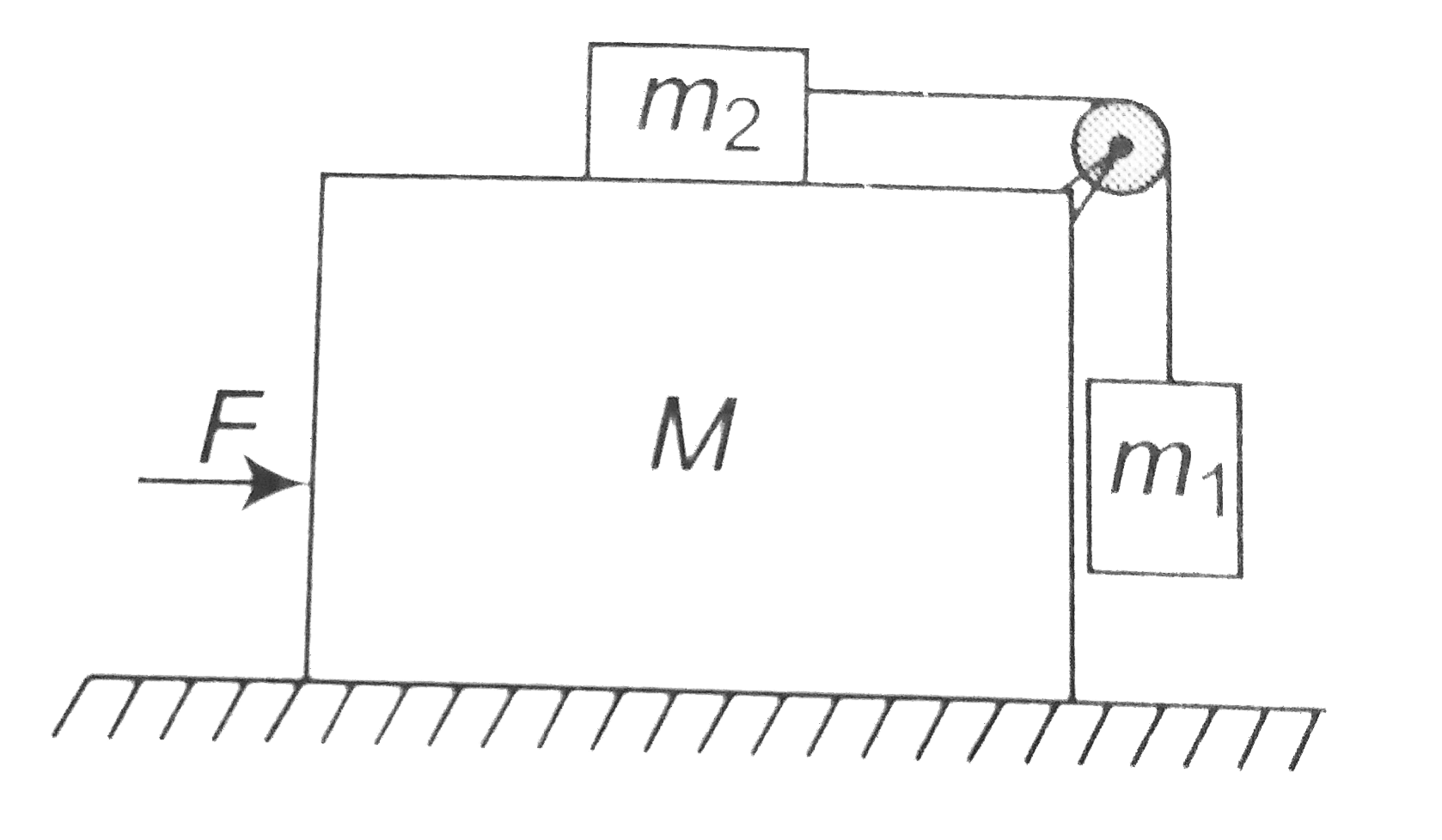 AF=m2m1(m1+m2+M)gBF=m1m2(m1+m2+M)gCF=m1m2(m1+M)gDF=m2m1(m1+M)g
AF=m2m1(m1+m2+M)gBF=m1m2(m1+m2+M)gCF=m1m2(m1+M)gDF=m2m1(m1+M)gA board of mass m = 1 kg lies on a table and a weight of M = 2 kg on the board. What minimum force F must be applied on the board in order to pull it out from under the road ? The coefficient of friction between board and table is μ2=0.5 : (Take g=10m/s2)
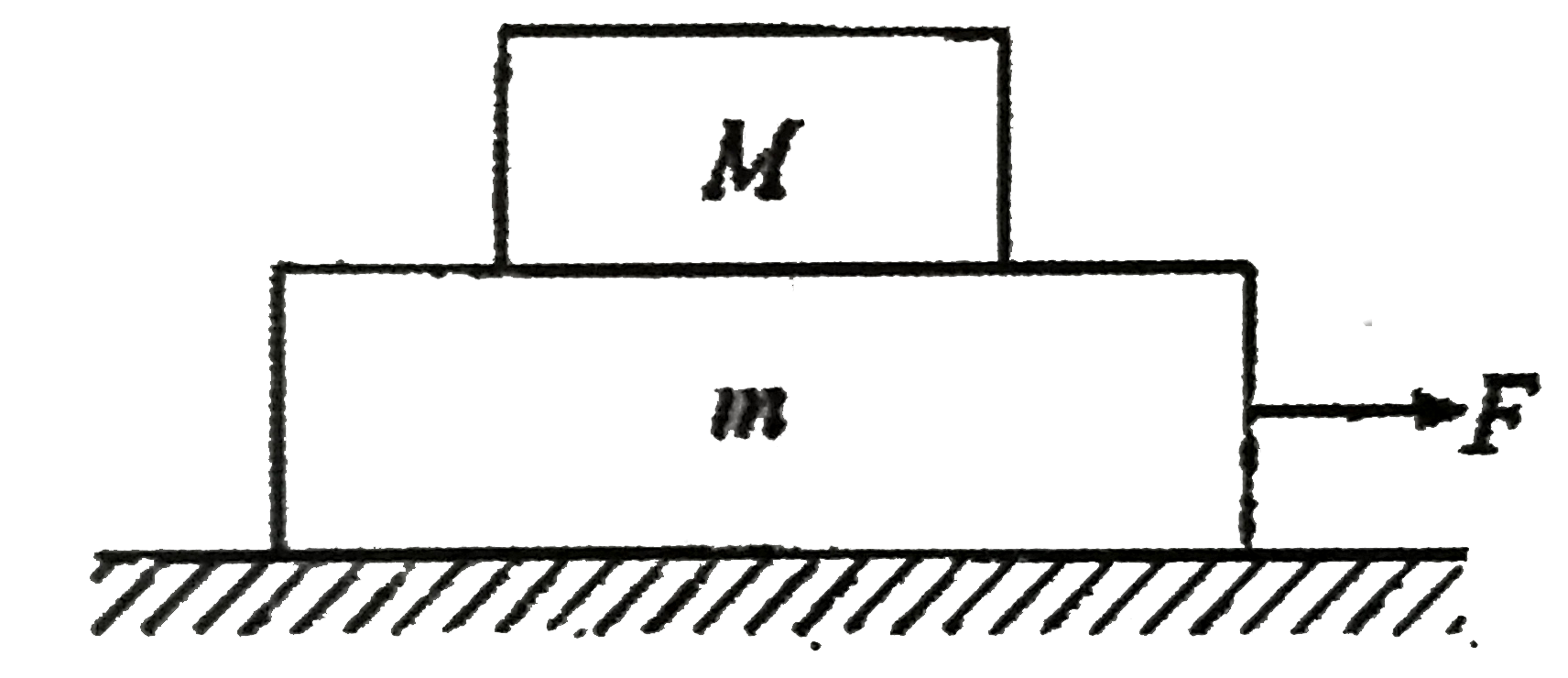 A7.5 NB15 NC22.5 ND30 N
A7.5 NB15 NC22.5 ND30 N
Figure-2.52 shows a box of mass m is placed on a wedge of mass M on a smooth surface. How much force F is required to be applied on M so that during motion m remains at rest on its surface
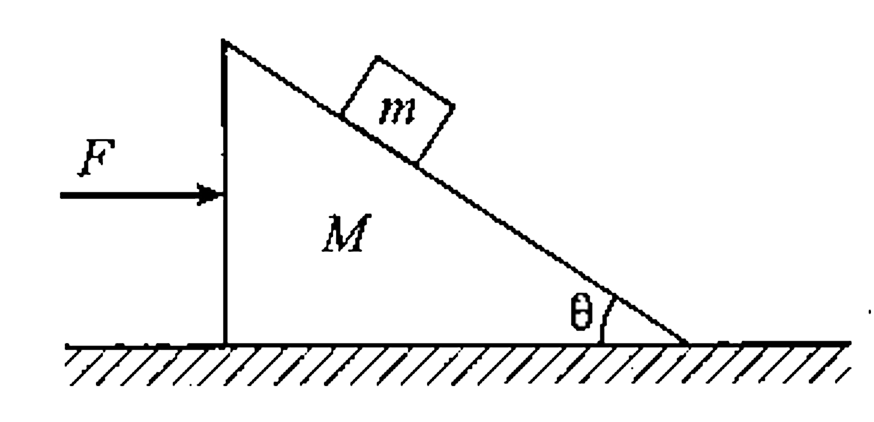
View SolutionA right-angled triangular block of mass M rests on a horizontal table . The inclination of the block is 30∘ with the table . A cubical block of mass m is placed on the incline of the block . What horizontal force must be applied on M so that m may remain stationery relative to the block ?
[Hint: Apply d' Alember's principal and consider free-body diagrams of m and the system ( m+ M).]
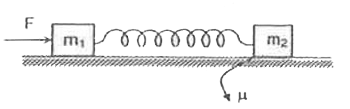
View SolutionFor Q. 25 find the minimum constant force to be applied to body of mass m1 in order to shift body of mass m2. Take m1=m2=10kg,μ=0.5
View SolutionTwo blocks of masses m1 and m2 are connected by a spring of stiffness k. The coefficient of friction between the blocks and the surface is μ. Find the minimum constant force F to be applied to m1 in order to just slide the mass m2.
View SolutionThree block of masses m1,m2 and m3 kg are placed in contact with each other on a frictionless table. A force F is applied on the heaviest mass m1, the acceleration of m2 will be

View Solution

