A 100 g mass stretches a particular spring by 9.8 cm, when suspended vertically from it. How large a mass must be attached to the spring if the period of vibration is to be 6.28 s?
1000g
105g
107g
`10^(4)g`
The correct Answer is:D
Step by step video, text & image solution for A 100 g mass stretches a particular spring by 9.8 cm, when suspended vertically from it. How large a mass must be attached to the spring if the period of vibration is to be 6.28 s? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- OSCILLATIONSBook:AAKASH INSTITUTEChapter:OSCILLATIONSExercise:Assignment (Section - B) (OBJECTIVE TYPE QUESTIONS)
Explore 30 Videos
- OSCILLATIONSBook:AAKASH INSTITUTEChapter:OSCILLATIONSExercise:Assignment (Section C) (PREVIOUS YEARS QUESTIONS)
Explore 43 Videos
- OSCILLATIONSBook:AAKASH INSTITUTEChapter:OSCILLATIONSExercise:Exercise
Explore 20 Videos
- NUCLEIBook:AAKASH INSTITUTEChapter:NUCLEIExercise:ASSIGNMENT (SECTION-D)
Explore 10 Videos
- PHYSICAL WORLDBook:AAKASH INSTITUTEChapter:PHYSICAL WORLDExercise:ASSIGNMENT (Section-B)
Explore 5 Videos
Similar Questions
A force of 6.4 N stretches a vertical spring by 0.1m. Find the mass that must be suspended from the spring so that it oscillates with a period of π/4
second.
View SolutionA force of 6.4 N stretches a vertical spring by 0.1 m. The mass (in kg) that must be suspended from the spring so that it oscillates with a time period of π4 second.
View Solution
Knowledge Check
A spring elongated by length 'L' when a mass 'M' is suspended to it. Now a tiny mass 'm' is attached and then released, its time period of oscillation is -
A2π√(M+m)lMgB2π√mlMgC2π√L/gD2π√Ml(m+M)gA body of mass m is suspended from three springs as shown in figure. If mass m is displaced slightly then time period of oscillation is
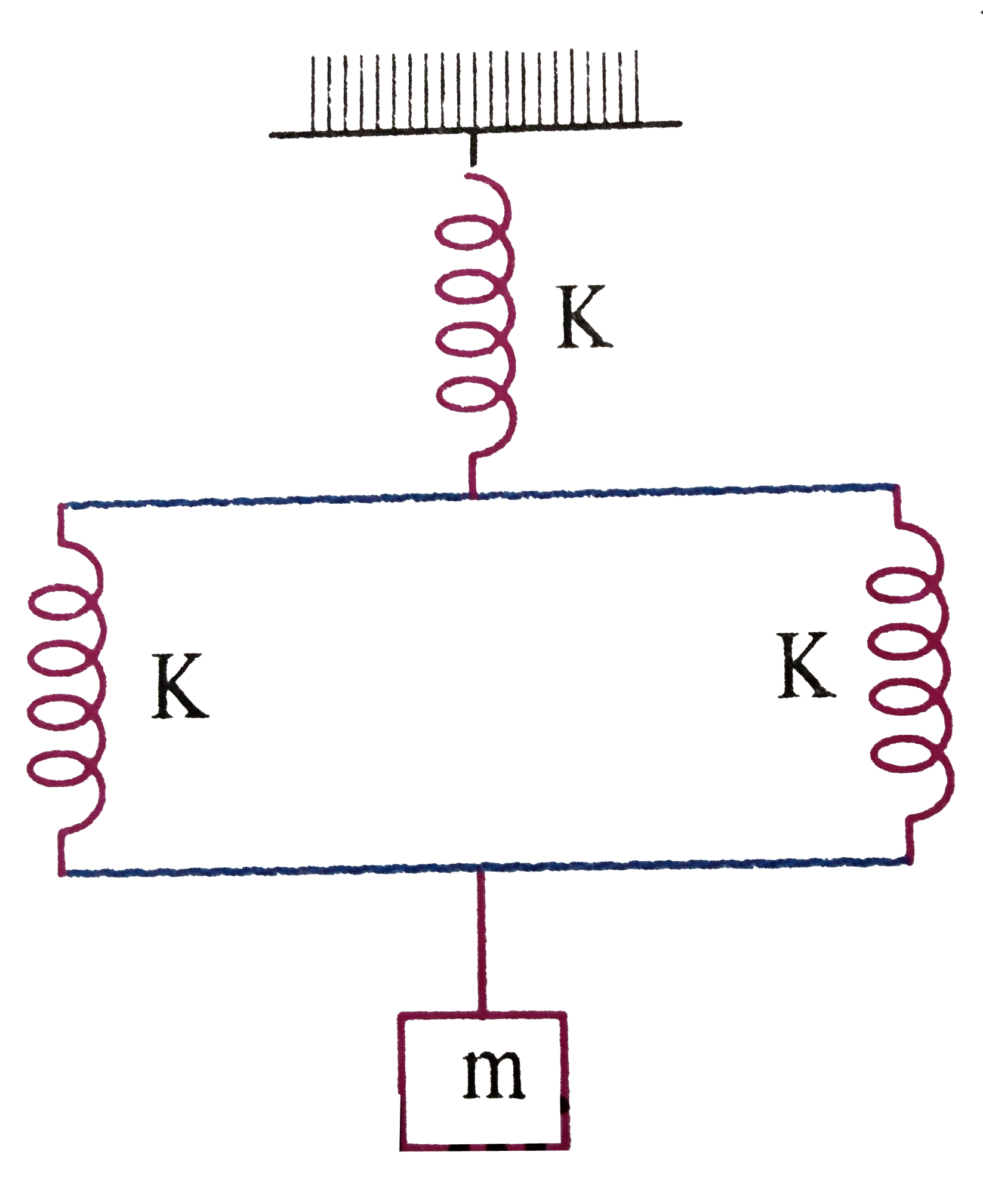 A2π√m3KB2π√3m2KC2π√2m3KD2π√3Km
A2π√m3KB2π√3m2KC2π√2m3KD2π√3KmA force of 6.4N stretched a vertical spring by 0.1m .The mass that must be suspended from the spring so that it oscillates with a time period of π/4 second
Aπ4kgB4πkgC1kgD10kg
Two springs are joined and attached to a mass of 16 kg. The system is then suspended vertically from a rigid support. The spring constant of the two spring are k1andk2 respectively. The period of vertical oscillations of the system will be
View SolutionIf the period of oscillation of mass m suspended from a spring is 2 s, then the period of mass 4 m will be
View SolutionA mass suspended on a vertical spring oscillates with a period of 0.5s. When the mass is allowed to hang at rest, the spring is stretched by
View SolutionWhen a mass m is hung on a spring, the spring stretched by 6 cm. If the loaded spring is pulled downward a little and released, then the period of vibration of the system will be
View SolutionTwo springs are joined and attached to a mass of 16 kg. The system is then suspended vertically from a rigid support. The spring constant of the two springs are K1 and K2 respectively. The period of vertical oscillations of the system will be:
View Solution

