A uniform disc of mass m and radius r is suspended through a wire attached to its centre. If the time period of the torsional oscillations be T, what is the torsional constant of the wire?
2π√3Rg
2π√R3g
2π√2R3g
2π√3R2g
The correct Answer is:D
Step by step video, text & image solution for A uniform disc of mass m and radius r is suspended through a wire attached to its centre. If the time period of the torsional oscillations be T, what is the torsional constant of the wire? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- OSCILLATIONSBook:AAKASH INSTITUTEChapter:OSCILLATIONSExercise:Assignment (Section - B) (OBJECTIVE TYPE QUESTIONS)
Explore 30 Videos
- OSCILLATIONSBook:AAKASH INSTITUTEChapter:OSCILLATIONSExercise:Assignment (Section C) (PREVIOUS YEARS QUESTIONS)
Explore 43 Videos
- OSCILLATIONSBook:AAKASH INSTITUTEChapter:OSCILLATIONSExercise:Exercise
Explore 20 Videos
- NUCLEIBook:AAKASH INSTITUTEChapter:NUCLEIExercise:ASSIGNMENT (SECTION-D)
Explore 10 Videos
- PHYSICAL WORLDBook:AAKASH INSTITUTEChapter:PHYSICAL WORLDExercise:ASSIGNMENT (Section-B)
Explore 5 Videos
Similar Questions
A uniform disc of radius r is to be suspended through a small hole made in te disc. Find the minimum possible time period of the disc for small oscillations. What should be the distance of the hole from the centre for it to have minimum time period?
View SolutionA uniform disc of radius 5.0 cm and mass 200g is fixed at its centre to a metal wire, the other end of which is fixed with a clamp. The hanging disc is rotated about the wire through an angle and is released. If the disc makes torsional oscillations with time period 0.20s, find the torsional constant of the wire.
View Solution
Knowledge Check
For a uniform ring of mass M and radius R at its centre
Afield and potential both are zeroBfield is zero but potential is GMRCfield is zero but potential is −GM/RDmagnitude of field is GMR2 and potential −GMRA uniform thin ring of radius R and mass m suspended in a vertical plane from a point in its circumference. Its time period of oscillation is
A2π√rgB2pi sqrt((5 R)/(3 g))C2π√7R5gD2π√2R5gA uniform semi-circular disc of mass m and radius r is suspended as shown in the figure. If T is the time period of small osciallations about an axis passing through point of supension and perpendicular to plane of disk. Then T is equal to
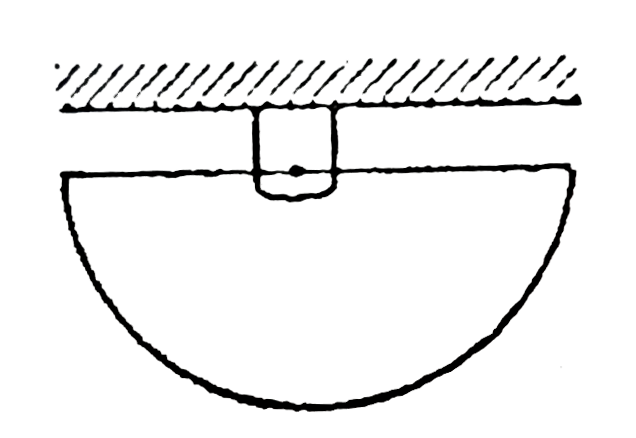 A2π√3r8gB2π√3rπ8gC2π√2rπ9gD2π√2r9g
A2π√3r8gB2π√3rπ8gC2π√2rπ9gD2π√2r9g
A uniform of radius 5.0cm and mass 200g is fixed at its centre to a metal wire , the other end of which is fixed to a celling. The hanging disc is rotate about the wire through an angle and is released. If the disc makes torsional oscillations with time period 0.20s , find the torsional constant of the wire.

View SolutionA circular disc of mass 12 kg is suspended by a wire attached to its centre. The wire is twisted by rotating the disc and then released, so that the time period of torsional oscillation is 2 s. If the radius of the disc is 10 cm, then calculate the torsional spring constant of the wire.
View SolutionA circular disc of mass 10kg is suspended by a wire attahced to its centre. The wire is twisted by rotating the disc and released. The period of torsional oscillations is found to be 1.5s. The radius of the disc is 15cm. Determing the torsional spring constant of the wire. (Torsional spring constant α is definied by the relation J=−αθ, where J is the restoring coubple and θ the angle of twist.
View SolutionA disc of radius R is suspended from its circumference and made to oscillate. Its time period will be:
View SolutionA uniform thin ring of radius R and mass m suspended in a vertical plane from a point in its circumference. Its time period of oscillation is
View Solution

