Derive the expression for magnetic field at a point on the axis of a circular current loop. Solution in Kannada
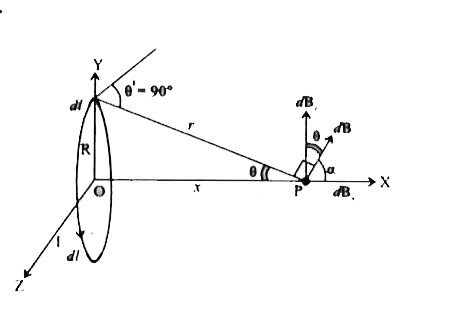
Let R be the radius of a current loop , carrying current I . Let R be a point on the axis of a conductor . Let dB be magnetic field at P , due to a current element .idl. .
From the figure , θ+α=90∘, so that α=90∘−θ and cosα=cos(90∘−θ)
=sinθ=R2(R2+x2)12...(1)
Let dBx be the horizontal component of dB.
Applying Biot-Savart.s law ,
we write
d→B=(μ04π)I(d→l×→r)r3
i.e., dB=(μ04π)Irdlr3sinθ . where θ.=90∘
i.e., dB=(μ04π)Irdlr3=(μ04π)Idlr2 ...(2)
Component of dB along the horizontal is dBx=dBcosα
or dBx=dBsinθ=(μ04π)Idlr2sinθ.
By using ...(1)
we write
dBx=(μ04π)Idlr2Rr=(μ04π)IdlR(R2+x2)32....(3)
or integrating
Bx=∫dBx=∫(μ04π)IR(R2+x2)32dl
i.e., Bx=(μ04π)IR(R2+x2)32(2πR)
where ∫dl=2πR
or
Bx=(μ04π)⎛⎜⎝2πIR2(R2+x2)32⎞⎟⎠ˆi,dBy=0
For a circular loop and at the centre , x=0 .
→B0=(μ04π)(2πlR)ˆi
For a circular conductor containing n turns ,
Bxˆi=(μ04π)2πnIR2(R2+x2)32ˆi
and at the centre ,
B0ˆi=(μ04π)(2πnIR)ˆi
Topper's Solved these Questions
- BOOK - SUBHASH PUBLICATIONCHAPTER - ANNUAL EXAM QUESTION PAPER -MARCH -2017 EXERCISE - PART -D12videos
ANNUAL EXAM QUESTION PAPER -MARCH -2017
- BOOK - SUBHASH PUBLICATIONCHAPTER - ANNUAL EXAMINATION QUESTION PAPER (WITH ANSWER) MARCH 2018EXERCISE - Part-C11videos
ANNUAL EXAMINATION QUESTION PAPER (WITH ANSWER) MARCH 2018
Similar Questions
Deduce the condition for balance of a wheatstone's bridge using Kirchoffs rules .
10:05View SolutionMention any three properties of an electric charge.
View SolutionUse Biot-Savart law to derive the expression for the magnetic field on the axis of a current carrying circular loop of radius R . Draw the magnetic field lines due to circular wire carrying current I .
04:57View SolutionDerive an expression for the magnetic field at a point on the axis of a current carrying circulat loop.
04:25View SolutionUsing Biot-Svart's law, derive the expression for the magnetic field in vector form at a point on the axis of a circular current loop.
View SolutionDerive the expression for magnetic field at a point on the axis of a circular current loop.
04:25View SolutionUsing Biot Savart's law, derive the expression for the magnetic field at a point on the axis of a circular current loop.
02:11View SolutionDerive the expression for magnetic field at a point on the axis of a circular current loop .
04:25View SolutionGive the expression for magnetic field at a point on the axis of a short magnetic dipole.
04:25View SolutionDerive the expression for magnetic field at a point on the axis of a circular current loop.
04:25View SolutionDerive the expression for magnetic field at a point on the axis of a circular current loop.
04:47View SolutionDerive the expression for magnetic field at a point on the axis of a circular current loop.
05:26View SolutionDerive an expresion for the magnetic field at any point on the axis of a circular current loop.
04:25View SolutionUsing Biot Savart’s law derive an expression for the magnetic field due to a circular current carrying loop at any point on its axis.
02:18View SolutionDerive the expression for magnetic field at a point on the axis of a circular current loop.
11:29View Solution

