Derive the expression for magnetic field at a point on the axis of a circular current loop. Solution in Kannada
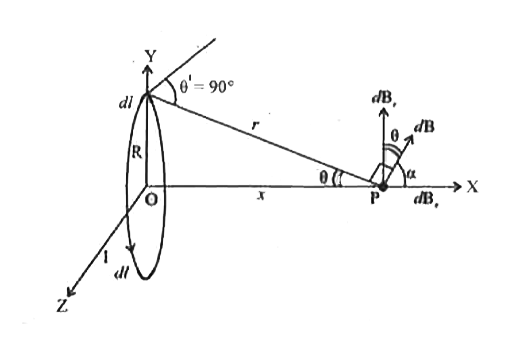
Let R be the radius of a current loop , carrying current I. Let R be a point on the axis of a conductor .Let dB be magnetic field at P , due to a current element .idl.
From the figure ,θ+α=90∘, so that α=90∘−θ
and codα=cos(90∘−θ)=sinθ=R2(R2+x2)12
let dBx be the horizontal component of dB .
Applying Biot - Savart.s law ,
We write d→B=(μ04π)I(d→l×→r)r3
i.e.,dB=(μ04π)Irdlr3sinθ. where θ.=90∘
i.e.,dB=(μ04π)irdlr3=(μ04π)idlr2
component of dB along the horizontal is dBX=dBcosα
or dBx=dBsinθ=(μ04π)idlr2sinθ.
By using (1) we write
dBX=(μ04π)Idlr2Rr=(μ04π)R(R2+x2)32.... (3)
or integrating
Bx=∫dBX=∫(μ04π)IR(R2+x2)32dl
i.e.,Bx=(μ04π)IR(R2+x2)32(2πR)
Where ∫dl=2πRor
Bx=(μ04π)⎛⎜⎝2πIR2(R2+x2)32⎞⎟⎠ tesl and
→b=Bxˆi=(μ04π)⎛⎜⎝2πIR2(R2+x2)32⎞⎟⎠ˆi,dBy=0
For a circular loop , and at the centre , x=0,
→B0=(μ04π)(2πlR)ˆi
for a circular conductor containing n turns ,
Bxˆi=(μ04π)2πnIR2(R2+x2)32ˆi and at the centre ,
B0ˆi=(μ04π)(2πnlR)ˆi.
Topper's Solved these Questions
- ANNUAL EXAM QUESTION PAPER -MARCH -2017 Book:SUBHASH PUBLICATIONChapter:ANNUAL EXAM QUESTION PAPER -MARCH -2017 Exercise:PART -C
Explore 8 Videos
- ALTERNATING CURRENT Book:SUBHASH PUBLICATIONChapter:ALTERNATING CURRENT Exercise:NUMERICALS WITH SOLUTIONS
Explore 34 Videos
- ANNUAL EXAM QUESTION PAPER MARCH 2018Book:SUBHASH PUBLICATIONChapter:ANNUAL EXAM QUESTION PAPER MARCH 2018Exercise:QUESTION
Explore 38 Videos
Similar Questions
Obtain the relation between electric field and electric potential due to a point charge.
View SolutionA 220 AC voltage source is connected across a pure inductor of inductance 0.5 H. Find the current through the inductor, if the frequency of the source is
100 Hz
View SolutionWhat is an equipotential surface ?
View SolutionUse Biot-Savart law to derive the expression for the magnetic field on the axis of a current carrying circular loop of radius R . Draw the magnetic field lines due to circular wire carrying current I .
View SolutionDerive an expression for the magnetic field at a point on the axis of a current carrying circulat loop.
View SolutionUsing Biot-Svart's law, derive the expression for the magnetic field in vector form at a point on the axis of a circular current loop.
View SolutionDerive the expression for the magnetic field on the axis of a circular current loop , using Biot-Savart's law.
View SolutionDerive the expression for magnetic field at a point on the axis of a circular current loop.
View SolutionUsing Biot Savart's law, derive the expression for the magnetic field at a point on the axis of a circular current loop.
View SolutionGive the expression for magnetic field at a point on the axis of a short magnetic dipole.
View SolutionDerive the expression for magnetic field at a point on the axis of a circular current loop.
View SolutionDerive the expression for magnetic field at a point on the axis of a circular current loop.
View SolutionDerive the expression for magnetic field at a point on the axis of a circular current loop.
View SolutionDerive an expresion for the magnetic field at any point on the axis of a circular current loop.
View SolutionUsing Biot Savart’s law derive an expression for the magnetic field due to a circular current carrying loop at any point on its axis.
View Solution