The area between x=y2and x=4is divided into two equal parts by the linex=a, find the value of a.
Video Solution
Text Solution
The graph of y2=4ax is symmetric about X-axis which is shown below. x=a lies between the lines x=0 and x=4. According to the given condition.
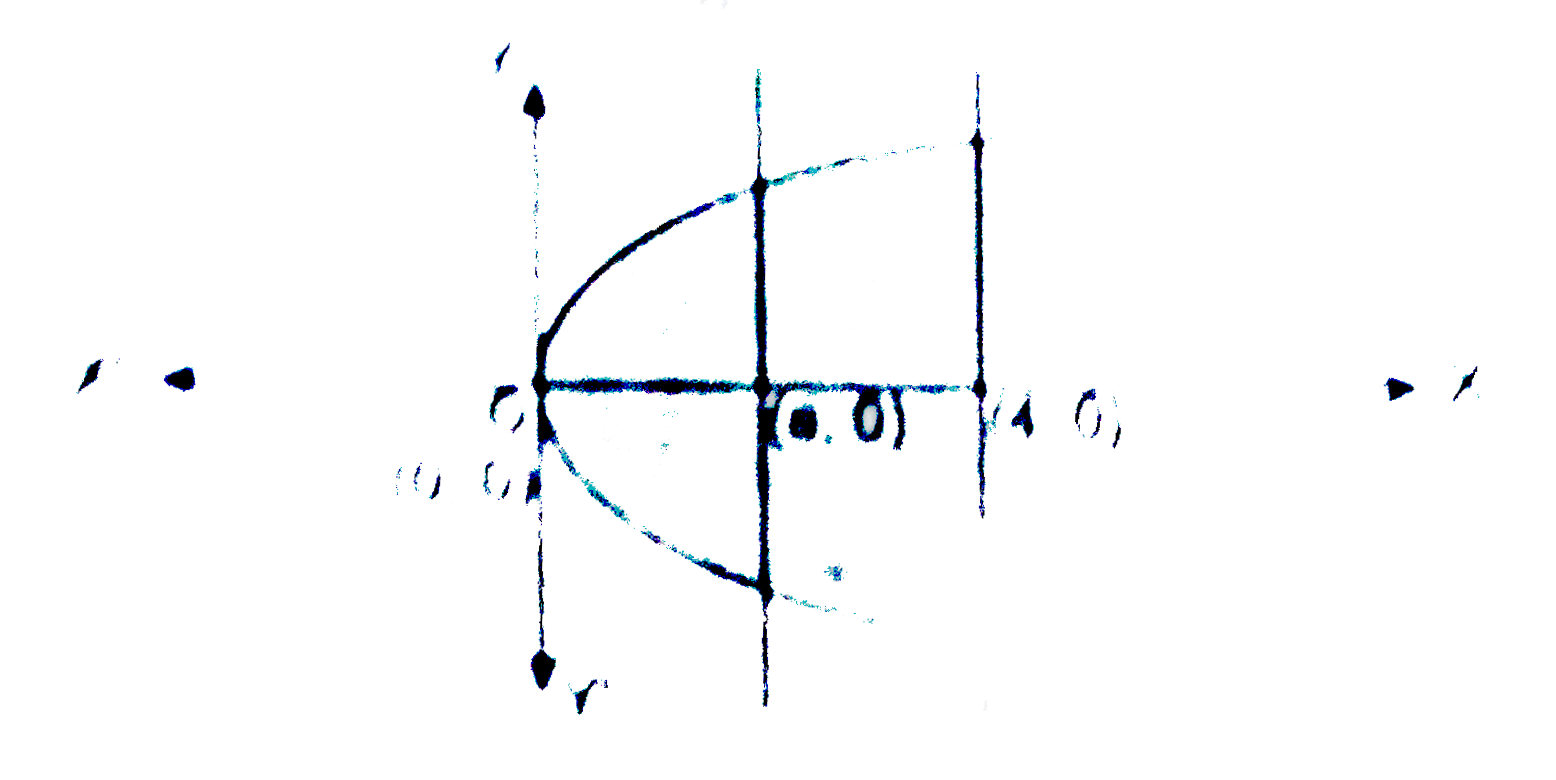
2∫a0ydx=2∫4aydx
⇒∫a02√a√xdx=∫4a2√a√xdx
⇒23[x3/2]a0=23[x3/2]4a
⇒a3/2=43/2−a3/2
⇒2a3/2=8⇒a3/2=4
⇒a=(4)2/3
|
Topper's Solved these Questions
- APPLICATIONS OF INTEGRALSBook:NAGEEN PRAKASHANChapter:APPLICATIONS OF INTEGRALSExercise:Exercise 8.2
Explore 7 Videos
- APPLICATIONS OF INTEGRALSBook:NAGEEN PRAKASHANChapter:APPLICATIONS OF INTEGRALSExercise:Miscellaneous Exercise
Explore 19 Videos
- APPLICATIONS OF INTEGRALSBook:NAGEEN PRAKASHANChapter:APPLICATIONS OF INTEGRALSExercise:Exercise 8 C Questions For Competitive Examinations
Explore 10 Videos
- APPLICATIONS OF DERIVATIVESBook:NAGEEN PRAKASHANChapter:APPLICATIONS OF DERIVATIVESExercise:Miscellaneous Exercise
Explore 24 Videos
- Continuity and DifferentiabilityBook:NAGEEN PRAKASHANChapter:Continuity and DifferentiabilityExercise:Miscellaneous Exercise
Explore 23 Videos
Similar Questions
Knowledge Check
The area between x=y2and x=4 is divided into two equal parts by the line x=a, find the value of a.
Aa=723Ba=223Ca=523Da=423The area bounded by the parabola x2=4y, the x-axis and the line x = 4 is divided into two equal area by the line x=α, then the value of α is
A21/3B22/3C24/3D25/3If the area bounded by the curve y=x2, the X-axis and the line x=21/3 is divided into two equal parts by the line x = a, then : a=
A16B1C23D31/3
The area bounded by the curve y=x2, the x-axis and the line x=213 is divided into two equal areas by the line x=k. The value of k is (A) 2−23 (B) 2−13 (C) 1 (D) 213−1
View SolutionThe circle x2+y2=4a2 is divided into two parts by the line x=3a2. Find the ratio of areas of these two parts.
View SolutionIf the area bounded by the curve x=y2 and the line x=4 gets divided by the line x=a into two equal halves, then find the value of a.
View SolutionThe area enclosed by the circle x2+(y+2)2=16 is divided into two parts by the x-axis. Find by integration, the area of the smaller part.
View SolutionIf the area bounded by the parabola x2=y and the line y = 4 is divided into equal parts by the line y = c, then : c =
View Solution

