Find the area of the region bounded by the ellipse x24+y29=1
Video Solution
Text Solution
Given curve is an ellipse which is symmetric about X-axis and both, as shown in the figure.
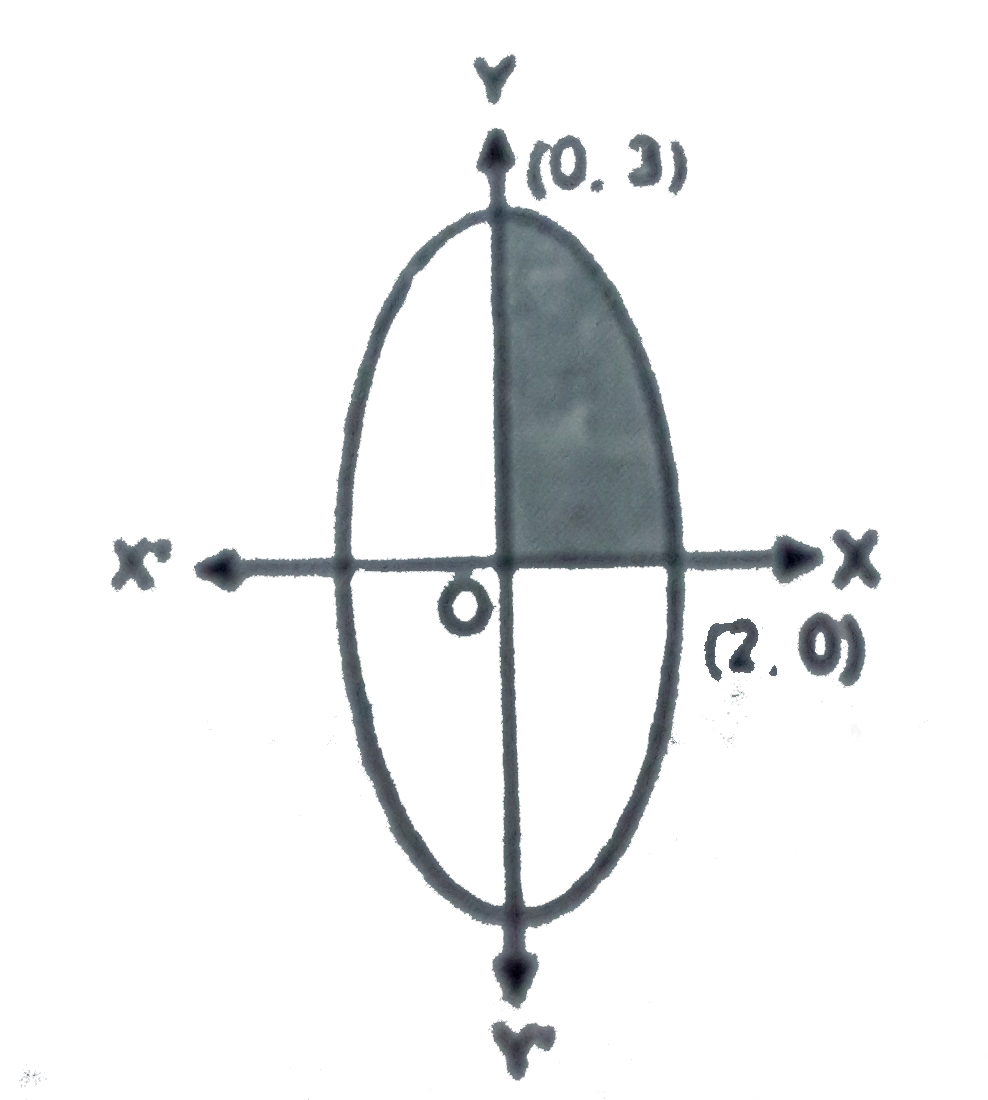
∴ Area bounded by ellipse
=4× (area of shaded region in first quadrant)
=4×∫20ydx=4∫2032√4−x2dx
=6∫20√22−x2dx
=6[x2√4−x2+222sin−1(x2)]20
=6{0+2sin−1(1)−0}
=6×2×(π2)
=6π sq. units.
|
Topper's Solved these Questions
- APPLICATIONS OF INTEGRALSBook:NAGEEN PRAKASHANChapter:APPLICATIONS OF INTEGRALSExercise:Exercise 8.2
Explore 7 Videos
- APPLICATIONS OF INTEGRALSBook:NAGEEN PRAKASHANChapter:APPLICATIONS OF INTEGRALSExercise:Miscellaneous Exercise
Explore 19 Videos
- APPLICATIONS OF INTEGRALSBook:NAGEEN PRAKASHANChapter:APPLICATIONS OF INTEGRALSExercise:Exercise 8 C Questions For Competitive Examinations
Explore 10 Videos
- APPLICATIONS OF DERIVATIVESBook:NAGEEN PRAKASHANChapter:APPLICATIONS OF DERIVATIVESExercise:Miscellaneous Exercise
Explore 24 Videos
- Continuity and DifferentiabilityBook:NAGEEN PRAKASHANChapter:Continuity and DifferentiabilityExercise:Miscellaneous Exercise
Explore 23 Videos
Similar Questions
Knowledge Check
Find the area of the region bounded by the ellipse x29+y24=1 in fourth quadrant.
A3π4 sq unitB3π2 sq unitC9π4 sq unitD4π7 sq unitFind the area of the region bounded by the ellipse x29+y24=1 in fourth quadrant.
A3π4 sq unitsB3π2 sq unitsC5π2 sq unitsDNone of theseThe area of the region bounded by the ellipse x225+y216=1 is
A20π sq unitsB20π2 sq unitsC16π2 sq unitsD25π sq units
Find the area of the region bounded by the ellipse :
(a)x29+y24=1
(b)(i)16x2+9y2=144
(ii) 4x2+25y2=1.
View SolutionFind the area of the smaller region bounded by the ellipse x29+y24=1 and the line x3+y2=1
View SolutionFind the area of the smaller region bounded by the ellipse x29+y24=1 and the line x3+y2=1.
View SolutionFind the area of the smaller region bounded by the ellipse x2a2+y2b2=1and the line xa+yb=1
View SolutionThe area of the region bounded by the ellipse x225+y216=1 is
View Solution

