Find the area of the smaller part of the circle x2+y2=a2cut off by the line x=a√2
Video Solution
Text Solution
Given x=a√2 ...(1)
and circle , x2+y2=a2 ...(2)
On solving , (a√2)2+y2=a2
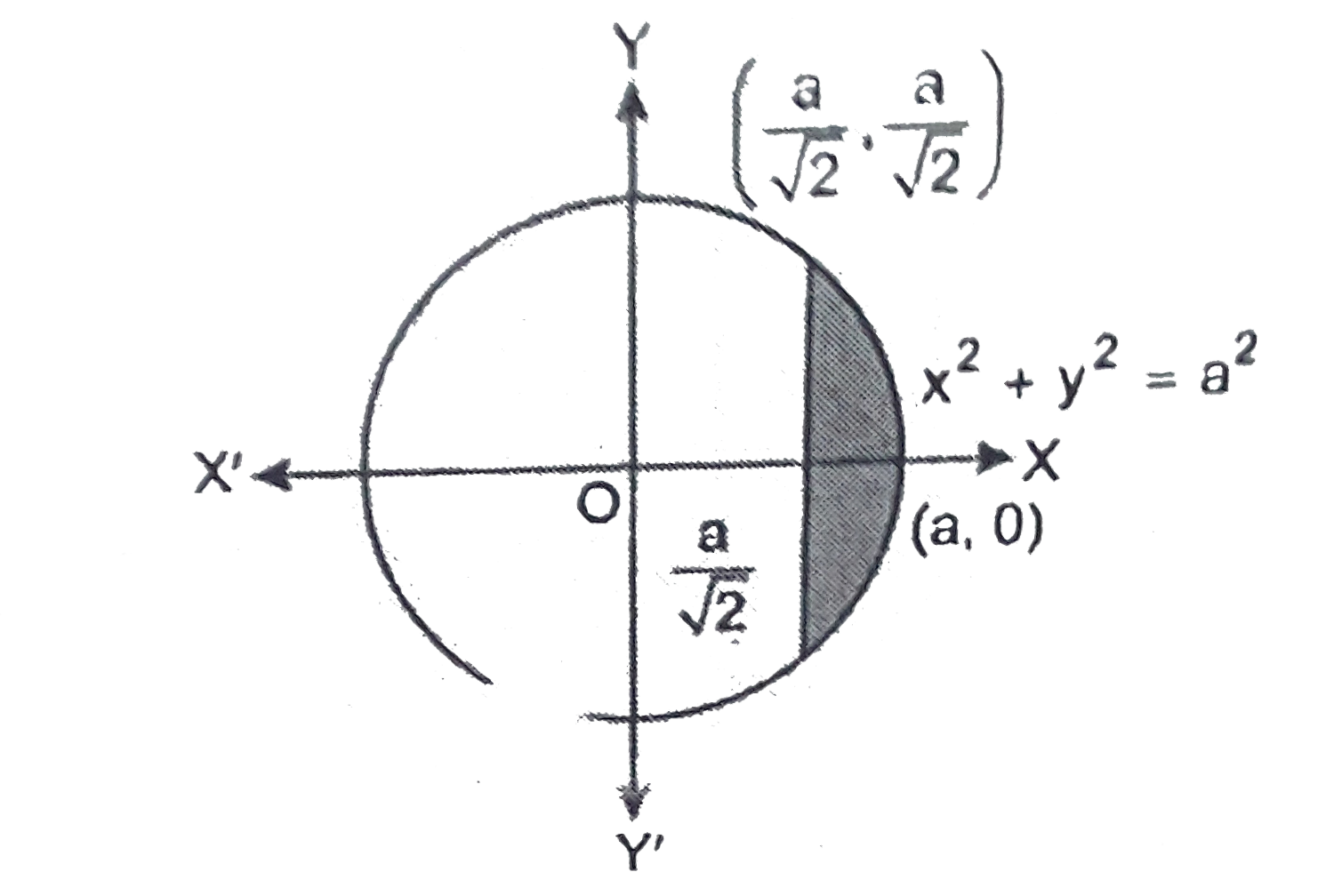
⇒y2=a21−a22=a22
⇒y=±a√2
y=a√2⇒x2=a2−(a22)
x2=a22⇒x=±a√2
∴ In first quadrant, the point of intersection is (a√2,a√2).
∴ Required area =2×(area of shaded region in first quadrant only)
=2∫aa√2√a2−x2dx
=2[xa√a2−x2+a22sin−1(xa)]aa/√2
=2[0+a22sin−1(1)−a2√2√a2−a22−a22sin−1(1√2)]
=2[a22(π2)−a2√2⋅a√2−a22(π4)]
=2[a2π4−πa28−a24]=(a2π4−a22)
=a22(π2−1) sq. unit.
|
Topper's Solved these Questions
- APPLICATIONS OF INTEGRALSBOOK - NAGEEN PRAKASHANCHAPTER - APPLICATIONS OF INTEGRALSEXERCISE - Exercise 8.2
7 Videos
- APPLICATIONS OF INTEGRALSBOOK - NAGEEN PRAKASHANCHAPTER - APPLICATIONS OF INTEGRALSEXERCISE - Miscellaneous Exercise
19 Videos
- APPLICATIONS OF INTEGRALSBOOK - NAGEEN PRAKASHANCHAPTER - APPLICATIONS OF INTEGRALSEXERCISE - Exercise 8 C Questions For Competitive Examinations
10 Videos
- APPLICATIONS OF DERIVATIVESBOOK - NAGEEN PRAKASHANCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Miscellaneous Exercise
24 Videos
- Continuity and DifferentiabilityBOOK - NAGEEN PRAKASHANCHAPTER - Continuity and DifferentiabilityEXERCISE - Miscellaneous Exercise
23 Videos
Similar Questions
Knowledge Check
The area of the smaller part of the circle x2+y2=2 cut off by the line x=1 is
Aπ2 sq. unitsB(π2−1) sq. unitsC(π2+1) sq. unitsD(π2−12) sq. unitsThe area of smaller part between the circle x2+y2=4 and the line x=1 is
A4π3−√3B8π3−√3C4π3+√3D5π3+√3
Prove that area of the smaller part of the cirlce x2+y2=a2 cut off by the line x=a√2 is a24(π−2) sq. units.
View SolutionThe area of the smaller portion of the circle x2+y2=4 cut off the line x+y=2 is
View SolutionThe area of smaller portion of the circle x2+y2=a2 cut off by the line x=a2(a>0) is
View SolutionThe area of the smaller portion of the circle x2+y2=4 cut-off by the line x=1 is (nπ−3√33)m2 .Find the value of n .
View SolutionFind the area of the portion of the parabola y2=4x cut off by the line y=x.
View SolutionThe range of values of r for which the point (−5+r√2,−3+r√2) is an interior point of the major segment of the circle x2+y2=16 , cut-off by the line x+y=2, is:
View Solution
