Draw a quadrilateral in the Cartesian plane, whose vertices are $(- 4, 5)$ , $(0, 7)$ , $(5, - 5)$ ,and $(- 4, - 2)$ . Also, find its area.

Video Solution

Text Solution

Verified by Experts

In the figure the vertices A = (-4,5), B = (0,7), C = (5,-5) and D = (-4,-2) of the quadrilateral are plotted on the graph.

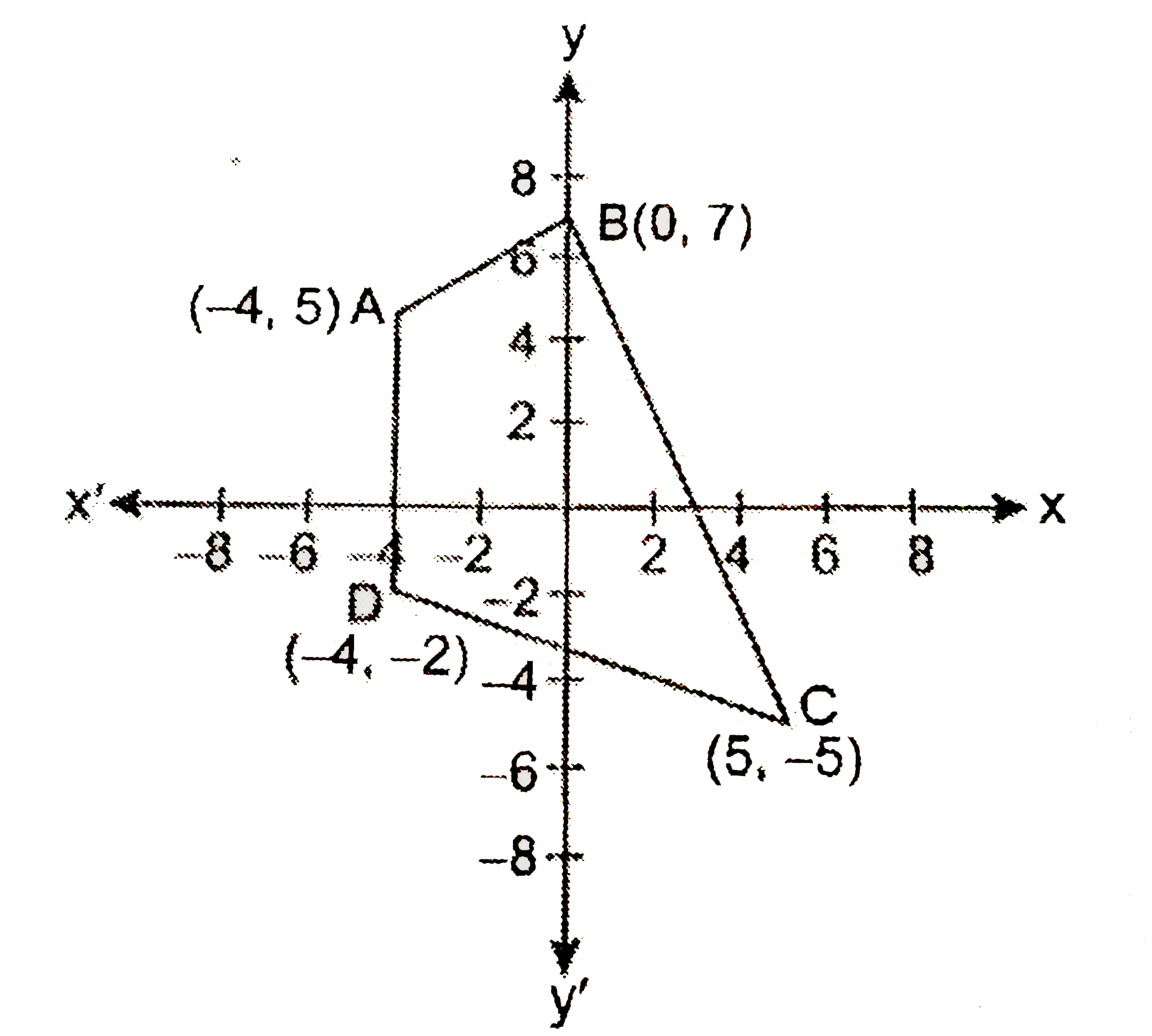
From the given vertices,
$x_{1} = - 4, y_{1} = 5$
$x_{2} = 0, y_{2} = 7$
$x_{3} = 5, y_{3} = - 5$
$x_{4} = - 4, y_{4} = - 2$
Join the diagonal AC.
Area of $Δ A B C$ ,
$= \frac{1}{2} [(x_{1} y_{2} + x_{2} y_{3} + x_{3} y_{1}) - (y_{1} x_{2} + y_{2} x_{3} + y_{3} x_{1})]$
$= \frac{1}{2} [{- 4 \times 7 + 0 \times (- 5) + 5 \times 5} - {5 \times 0 + 7 \times 5 + (- 5) \times (- 4)}]$
$= \frac{1}{2} [(- 28 + 0 + 25) - (0 + 35 + 20)]$
$= \frac{1}{2} [(- 3) - (55)]$
$= \frac{1}{2} (- 58) = 29 (neglecting negative sign)$
Area of $Δ A C D$
$= \frac{1}{2} [(x_{1} y_{3} + x_{3} y_{4} + x_{4} y_{1}) - (y_{1} x_{3} + y_{3} x_{4} + y_{4} x_{1})]$
$= \frac{1}{2} [{- 4 \times - 5 + 5 \times (- 2) + 5 \times (- 4)} - {5 \times 5 + (- 5) \times (- 4) + (- 2) \times (- 4)}]$
$= \frac{1}{2} [(20 - 10 - 20) - (25 + 20 + 8)]$
$= \frac{1}{2} [(- 10) - (53)]$
$= \frac{1}{2} [- 63] = \frac{63}{2} (neglecting negative sign)$
$= 31.5$
Therefore, are of quadrilateral ABCD
= Area of $Δ A B C$ + Area of $Δ A C D$
$= 29 + 31.5 = 60.5$ units
Therefore, are of quadrilateral ABCD = 60.5 units.

|

Updated on:21/07/2023

Class 11 MATHS STRAIGHT LINES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Find the area of quadrilateral whose vertices are (-4,5) , (0,7), (5,-5) and (-4-2)
A $54 \frac{1}{2}$ sq. units
B $56 \frac{1}{2}$ sq. units
C $58 \frac{1}{2}$ sq. units
D $60 \frac{1}{2}$ sq. units

NAGEEN PRAKASHAN-STRAIGHT LINES-Exercise

Home
Ask Doubt
Profile