The slope of a line is double of the slope of another line. If tangent of the angle between them is $\frac{1}{3},$ find the slopes of the lines.

Video Solution

Text Solution

Verified by Experts

Let the slope of first line be $m_{1}$ and slope of second line be $m_{2}$ .
If $θ$ is the angle between two lines then
$tan θ = ∣ ∣ ∣ \frac{m_{2} - m_{1}}{1 + m_{1} m_{2}} ∣ ∣ ∣$
But it is given that the tangent of angle $θ = \frac{1}{3}$
$\Rightarrow \frac{1}{3} = ∣ ∣ ∣ \frac{m_{2} - m_{1}}{1 + m_{1} m_{2}} ∣ ∣ ∣$ ....... $(1)$
$m_{1} = 2 m_{2}$ ....... $(2)$
Put the value of $m_{1}$ from equation $(2)$ to equation $(1)$ ,
$\frac{1}{3} = ∣ ∣ ∣ \frac{m_{2} - 2 m_{2}}{1 + 2 m_{2} \times m_{2}} ∣ ∣ ∣$
$\Rightarrow \frac{1}{3} = \frac{\pm m_{2}}{1 + 2 m_{2}^{2}}$
$\Rightarrow 2 m_{2}^{2} \pm 2 m_{2} + 1 = 0$
$\Rightarrow (2 m_{2} \pm 1) (m_{2} \pm 1) = 0$
$\Rightarrow m_{2} = \pm 1$ or $\pm \frac{1}{2}$
Then if $m_{2} = \pm 1$ then $m_{1} = \pm 2$ and if $m_{2} = \pm \frac{1}{2}$ then $m_{1} = \pm 1$
$∴$ Slope of a line $m_{1} = \pm 2$ or $\pm 1$
and slope of other line $m_{2} = \pm 1$ or $\pm \frac{1}{2}$
Therefore, slopes of the lines are ( $\pm 2$ or $\pm 1$ ) and ( $\pm 1$ or $\pm \frac{1}{2}$ ).

Updated on:21/07/2023

The slope of a line is 3 times the slope of the other line and the tangent of the angle between them is 4/13, sum of their slopes is equal to
A2
B4
C6
D8
Slope of a budget line is
AIncreaseing throghout
BDecreasing through out
CConstant throughout
DFluctuating through out
The slope of the given line is ,

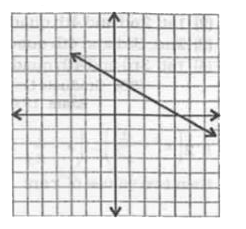APositive
BNegative
CUndefined
DZero