A body of mass 0.01 kg executes simple harmonic motion (SHM) about x=0 under the influence of a force shown in the figure. The period of the SHM is
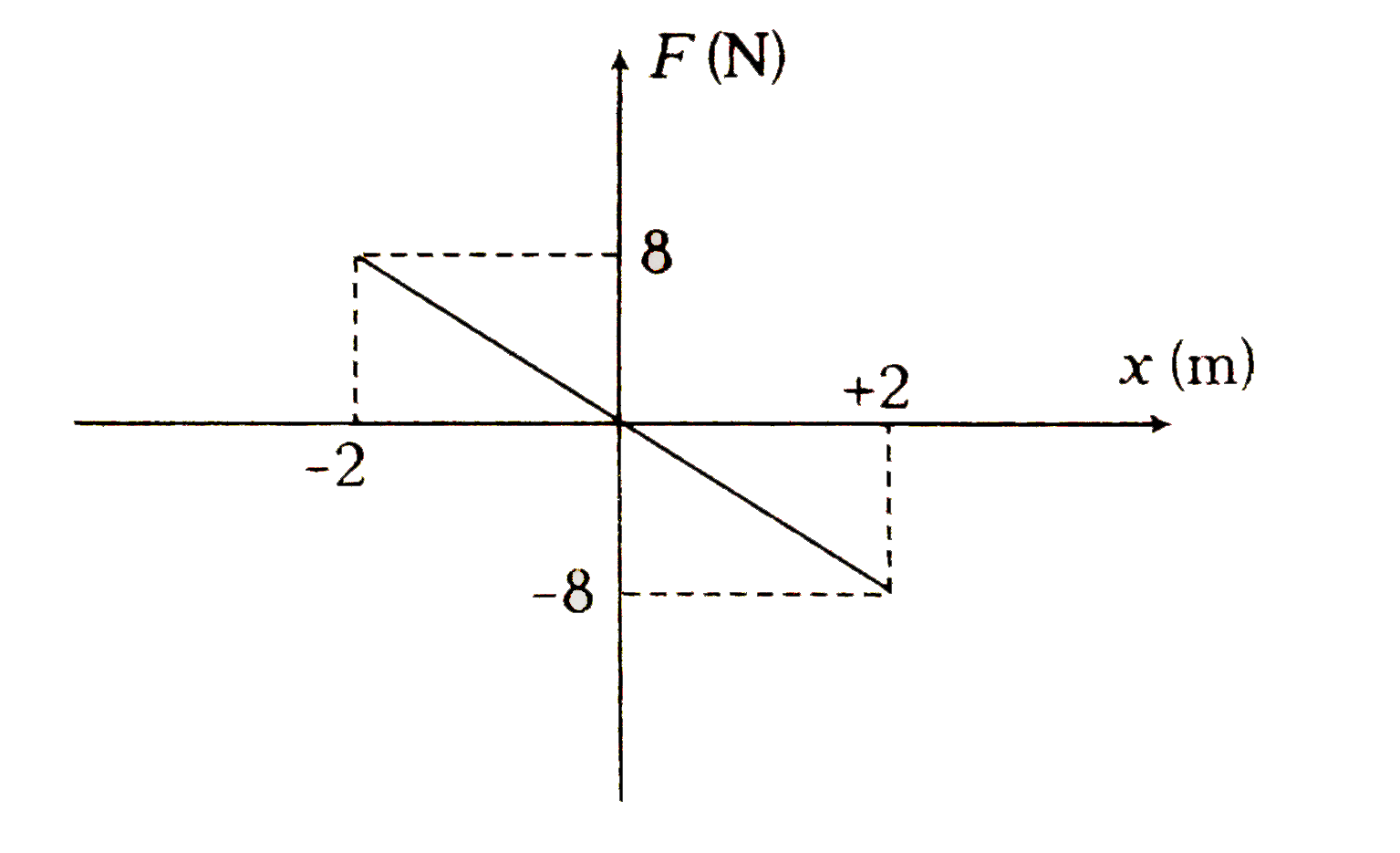
1.05 s
0.52 s
0.25 s
0.31 s
The correct Answer is:D
(d) From graph, slope K=Fx=82=4
T=2π√mk⇒T=2π√0.014=0.31s
Similar Questions
A body of mass 0.01 kg executes simple harmonic motion about x = 0 under the influence of a force as shown in figure. The time period of SHM is
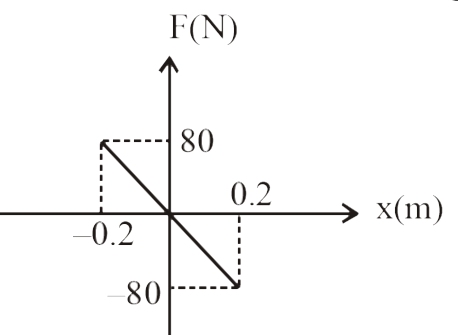 View Solution
View SolutionA block of mass 5 kg executes simple harmonic motion under the restoring force of a spring. The amplitude and the time period of the motion are 0.1 m and 3.14 s respectively. Fnd the maximum force exerted by the spring on the block.
View Solution
Knowledge Check
- Question 1 - Select One
A block of mass 2kg executes simple harmonic motion under the reading from at a spring .The angular and the time period of motion are 0.2cm and 2πsec respectively Find the maximum force execute by the spring in the block.
A0.05NB0.002NC0.003ND0.004N - Question 2 - Select One
A body executes simple harmonic motion under the action of a force F1 with a time period 45s . If the force is changed to F2, it executes SHM with time period 35s. If both the forces F1andF2 act simultaneously in the same direction on the body, its time period (in seconds) is
A1225B2425C3524D2512 - Question 3 - Select One
A body of mass 0.1 kg is executing a simple harmonic motion of amplitude 0.2 m. When the body passes through the mean position, its kinetic energy is 8×10−3 J. The initial phase of oscillation is 60. What is the equation of motion of the body ?
Ay=0.2sin(14+π3)By=0.2sin(4t+π3)Cy=0.2sin(12+π3)Dy=0.2sin(4t−π3)
A body is executing simple harmonic motion under the action of a force F1 with time period 1 s. The time period is 2s when body is acted by another force F3. What will be the total time period when both the forces are acting in same direction simultaneously ?
View SolutionA particle of mass 0.50kg executes a simple harmonic motion under a forve F=−(50n/m)x. If crosses the centre of oscillation with a speed of 10m/s, find the amplitude of the motion.
View SolutionA particle of mass 0.50 kg executes a simple harmonic motion under a force F=−(50Nm−1)x. If it crosses the centre of oscillation with a speed of 10ms−1, find the amplitude of the motion.
View SolutionA particle of mass 0.50 kg executes a simple harmonic motion under a force F = – (50 N/m)x. If it crosses the centre of oscillation with a speed of 10 m/s, find the amplitude of the motion.
View SolutionA block of mass 2 kg executes SHM on a smooth horizontal plane under the action of restoring force of a spring. If the amplitude and time period of oscillation are 0.05 m and π/5 second, the maximum force exerted by the spring on the block is
View Solution

