A body is executing simple harmonic motion under the action of a force F1 with time period 1 s. The time period is 2s when body is acted by another force F3. What will be the total time period when both the forces are acting in same direction simultaneously ?
To solve the problem, we will follow these steps:
Step 1: Understand the relationship between force and time period
The time period T of a body executing simple harmonic motion (SHM) is related to the force acting on it. The relationship can be expressed as:
T∝√1F
This means that the time period is inversely proportional to the square root of the force.
Step 2: Identify the forces and their corresponding time periods
From the problem, we know:
- For force F1, the time period T1=1 s.
- For force F3, the time period T3=2 s.
Step 3: Calculate the forces corresponding to the time periods
Using the relationship T∝√1F, we can express the forces in terms of the time periods:
F1=k⋅1T21=k⋅112=k
F3=k⋅1T23=k⋅122=k4
Thus, we can say:
F1=4F3
Step 4: Find the total force when both forces act together
When both forces F1 and F3 are acting in the same direction, the total force Ftotal is:
Ftotal=F1+F3=k+k4=4k4+k4=5k4
Step 5: Calculate the new time period when both forces are acting together
Using the relationship T∝√1F, we can find the new time period Ttotal:
1T2total=Ftotalk=5k4k=54
Thus,
T2total=45
Taking the square root gives:
Ttotal=√45=2√5≈0.894 seconds
Final Answer
The total time period when both forces are acting in the same direction simultaneously is approximately 0.89 seconds.
---
The time period T of a body executing simple harmonic motion (SHM) is related to the force acting on it. The relationship can be expressed as:
T∝√1F
This means that the time period is inversely proportional to the square root of the force.
From the problem, we know:
- For force F1, the time period T1=1 s.
- For force F3, the time period T3=2 s.
Using the relationship T∝√1F, we can express the forces in terms of the time periods:
F1=k⋅1T21=k⋅112=k
F3=k⋅1T23=k⋅122=k4
Thus, we can say:
F1=4F3
When both forces F1 and F3 are acting in the same direction, the total force Ftotal is:
Ftotal=F1+F3=k+k4=4k4+k4=5k4
Using the relationship T∝√1F, we can find the new time period Ttotal:
1T2total=Ftotalk=5k4k=54
Thus,
T2total=45
Taking the square root gives:
Ttotal=√45=2√5≈0.894 seconds
The total time period when both forces are acting in the same direction simultaneously is approximately 0.89 seconds.
Topper's Solved these Questions
- OSCILLATIONS Book:MODERN PUBLICATIONChapter:OSCILLATIONS Exercise:Competition File (Multiple choice questions)
Explore 20 Videos
- OSCILLATIONS Book:MODERN PUBLICATIONChapter:OSCILLATIONS Exercise:Competition File (Multiple choice questions) AIPMT/NEET other State Boards for Medical Entrance
Explore 14 Videos
- OSCILLATIONS Book:MODERN PUBLICATIONChapter:OSCILLATIONS Exercise:Revision Exercises (Long Answer Questions)
Explore 5 Videos
- MOTION IN A STRAIGHT LINE Book:MODERN PUBLICATIONChapter:MOTION IN A STRAIGHT LINE Exercise:CHAPTER PRACTICE TEST
Explore 16 Videos
- PHYSICAL WORLD Book:MODERN PUBLICATIONChapter:PHYSICAL WORLD Exercise:Revision exercises (Long answer questions)
Explore 6 Videos
Similar Questions
A body executes SHM under the influence of one force with a time period of 0.8second. It has a time period of 0.6 second udner the action of another force. Calculate the time period when both the force act in the same direction simultaneously.
View SolutionA particle is executing simple harmonic motion under the action of a force F with a time period 35s. When the force is changed to F', the time period of oscillation is 45s. When both the forces F and F' act simultaneously in the same direction on the body, time period in seconds in T=6a5b. COmpute the value of a + b.
View Solution
Knowledge Check
A body has a time period (4/5) s under the action of one force and (3/5) s under the action of another force. Then time period when both the forces are acting in the same direction simultaneously will be
A4/5sB5/4sC1sD12/25sA body has a time period (4/5) s under the action of one force and (3/5) s under the action of another force. Then time period when both the forces are acting in the opposite direction simultaneously will be
A4/5sB5/4sC1 sD12/5√7sA body executes simple harmonic motion under the action of a force F1 with a time period 45s . If the force is changed to F2, it executes SHM with time period 35s. If both the forces F1andF2 act simultaneously in the same direction on the body, its time period (in seconds) is
A1225B2425C3524D2512
A body of mass 0.01 kg executes simple harmonic motion about x = 0 under the influence of a force as shown in figure. The time period of SHM is
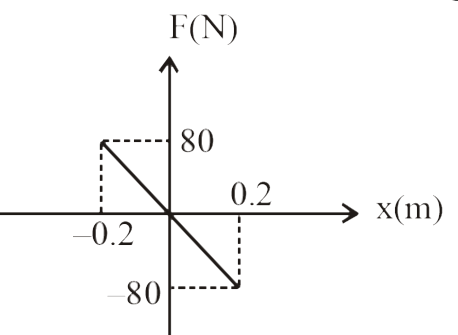
View SolutionA body has a time period T1 under the action of one force and T2 under the action of another force, the square of the time period when both the forces are acting in the same direction is
View SolutionA body of mass 0.01 kg executes simple harmonic motion (SHM) about x=0 under the influence of a force shown in the figure. The period of the SHM is
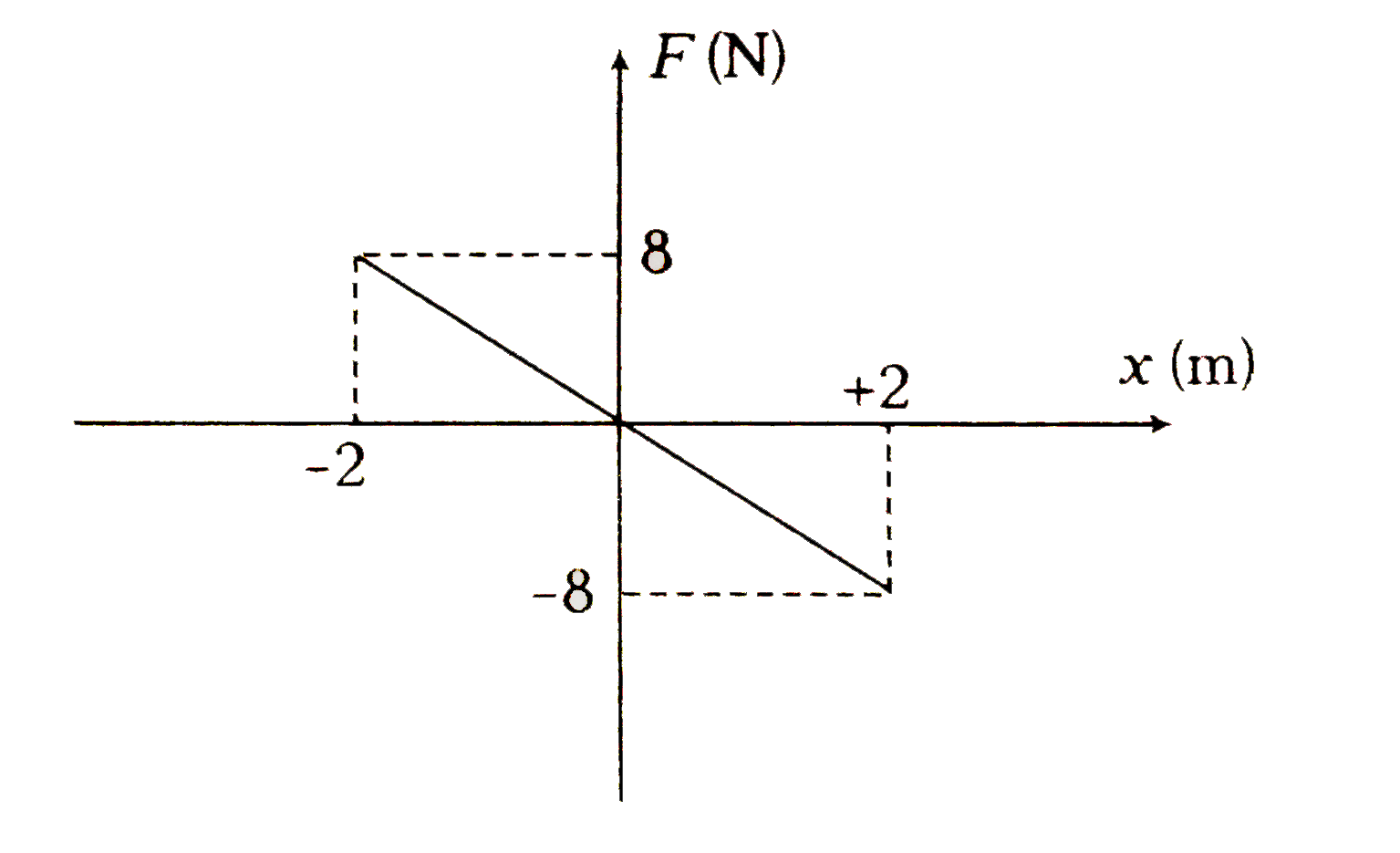
View SolutionA particle executing simple harmonic motion with time period T. the time period with which its kinetic energy oscillates is
View SolutionIf particle is excuting simple harmonic motion with time period T, then the time period of its total mechanical energy is :-
View Solution

