A body executes simple harmonic motion under the action of a force F1 with a time period 45s . If the force is changed to F2, it executes SHM with time period 35s. If both the forces F1andF2 act simultaneously in the same direction on the body, its time period (in seconds) is
1225
2425
3524
2512
The correct Answer is:A
To solve the problem, we need to find the time period of a body executing simple harmonic motion (SHM) when two forces, F1 and F2, act simultaneously. We know the time periods for each force acting alone, T1 and T2.
1. Identify the Given Time Periods:
- The time period for force F1 is T1=45 seconds.
- The time period for force F2 is T2=35 seconds.
2. Relate Time Period to Angular Frequency:
- The angular frequency ω is related to the time period T by the formula:
ω=2πT
- Therefore, we can express ω1 and ω2 for the two forces:
ω1=2πT1=2π45=10π4=5π2
ω2=2πT2=2π35=10π3
3. Calculate the Effective Angular Frequency:
- When both forces act simultaneously, the effective angular frequency ω can be found using the formula:
1T2=1T21+1T22
- First, calculate T21 and T22:
T21=(45)2=1625
T22=(35)2=925
4. Substitute into the Equation:
- Now substitute these values into the equation:
1T2=11625+1925=2516+259
5. Find a Common Denominator:
- The common denominator of 16 and 9 is 144:
2516=225144,259=400144
- Therefore,
1T2=225+400144=625144
6. Calculate T2:
- Taking the reciprocal gives:
T2=144625
7. Find T:
- Finally, take the square root to find T:
T=√144625=1225 seconds
Final Answer:
The time period when both forces F1 and F2 act simultaneously is 1225 seconds.
---
- The time period for force F1 is T1=45 seconds.
- The time period for force F2 is T2=35 seconds.
- The angular frequency ω is related to the time period T by the formula:
ω=2πT
- Therefore, we can express ω1 and ω2 for the two forces:
ω1=2πT1=2π45=10π4=5π2
ω2=2πT2=2π35=10π3
- When both forces act simultaneously, the effective angular frequency ω can be found using the formula:
1T2=1T21+1T22
- First, calculate T21 and T22:
T21=(45)2=1625
T22=(35)2=925
- Now substitute these values into the equation:
1T2=11625+1925=2516+259
- The common denominator of 16 and 9 is 144:
2516=225144,259=400144
- Therefore,
1T2=225+400144=625144
- Taking the reciprocal gives:
T2=144625
- Finally, take the square root to find T:
T=√144625=1225 seconds
The time period when both forces F1 and F2 act simultaneously is 1225 seconds.
Topper's Solved these Questions
Similar Questions
A particle is executing simple harmonic motion under the action of a force F with a time period 35s. When the force is changed to F', the time period of oscillation is 45s. When both the forces F and F' act simultaneously in the same direction on the body, time period in seconds in T=6a5b. COmpute the value of a + b.
View SolutionA body is executing simple harmonic motion under the action of a force F1 with time period 1 s. The time period is 2s when body is acted by another force F3. What will be the total time period when both the forces are acting in same direction simultaneously ?
View Solution
Knowledge Check
Due to some force F1 a body oscillates with period 4/5s and due to other force F2 it oscillates with period 3/5s. If both the forces acts simultaneously in same direction then new period is
A0.72sB0.64sC0.48sD0.36sDue to some force F1 a body oscillates with period 4/5s and due to other force F2 it oscillates with period 3/5s. If both the forces acts simultaneously in same direction then new period is
A0.72 sB0.64 sC0.48 sD0.36 sA body executes SHM under the influence of one force and has a period T1 seconds and the same body executes SHM with period T2 seconds when under the influence of another force. When both forces act simultaneously and in the same direction, then the time period of the same body (in seconds) is:
AT1+T2B√T21+T22C√T21+T22T1T2D ⎷T21T22(T21+T22)
A body of mass 0.01 kg executes simple harmonic motion about x = 0 under the influence of a force as shown in figure. The time period of SHM is
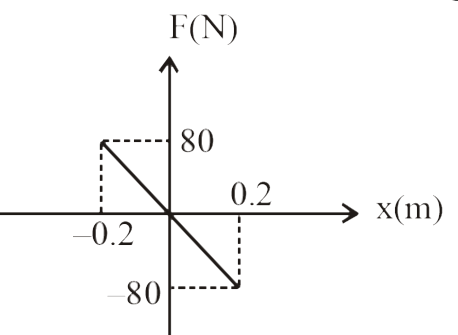
View SolutionA body executes SHM under the influence of one force with a time period of 0.8second. It has a time period of 0.6 second udner the action of another force. Calculate the time period when both the force act in the same direction simultaneously.
View SolutionA body of mass 0.01 kg executes simple harmonic motion (SHM) about x=0 under the influence of a force shown in the figure. The period of the SHM is
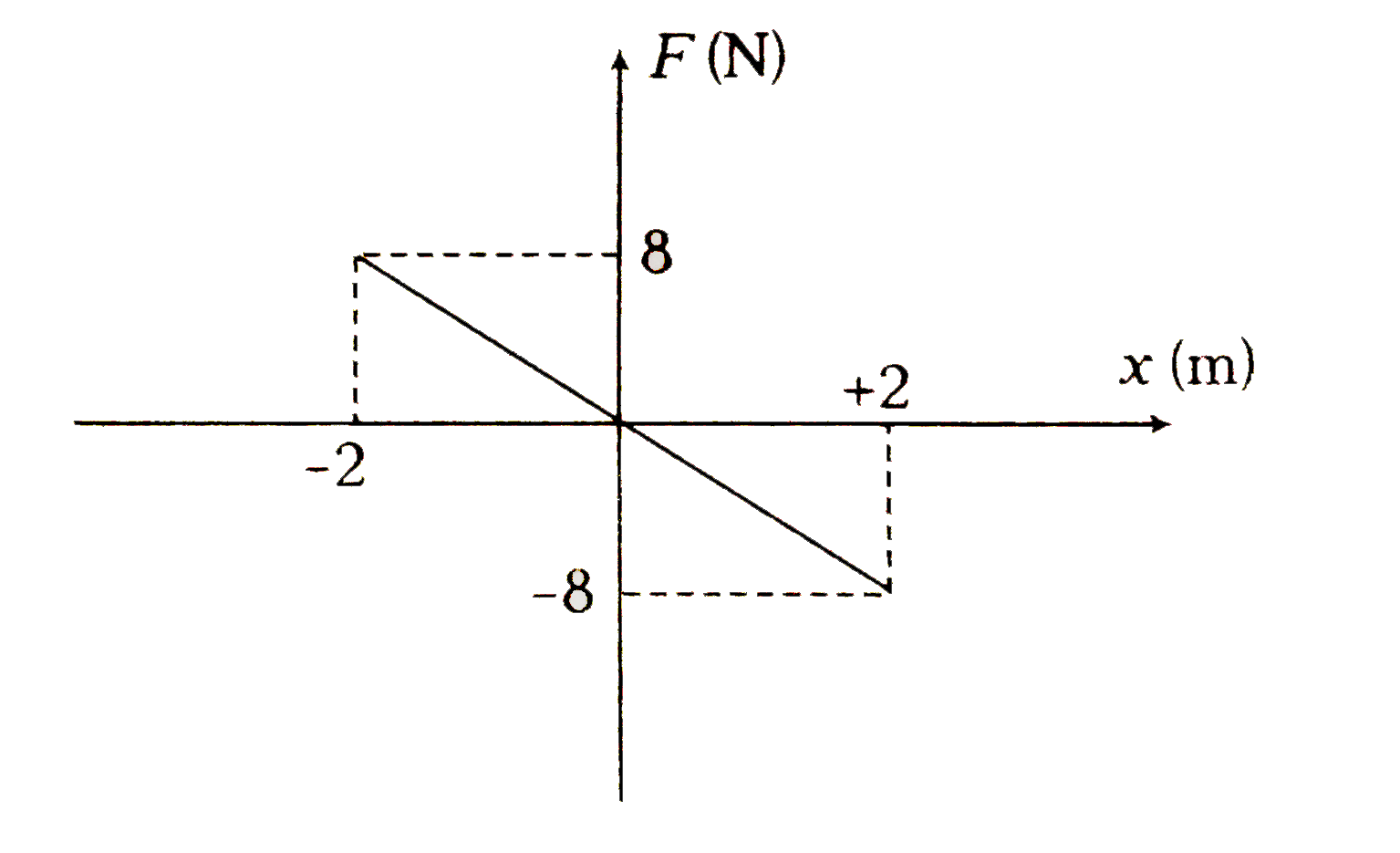
View SolutionA body has a time period (4/5) s under the action of one force and (3/5) s under the action of another force. Then time period when both the forces are acting in the same direction simultaneously will be
View SolutionA body has a time period T1 under the action of one force and T2 under the action of another force, the square of the time period when both the forces are acting in the same direction is
View Solution
