A dielectric circular disc of radius R carries a uniform surface charge density $σ$ . If it rotates about its exis with angular velocity $ω$ , the magnetic field at the cente of disc is :Solution in Telugu

A

$\frac{μ_{0} σ ω R^{2}}{2 π}$

B

$\frac{μ_{0} σ ω R}{2}$

C

$\frac{μ_{0} σ ω R^{2}}{4}$

D

$\frac{μ_{0} σ ω R^{2}}{2 \sqrt{2}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Let us assumed a ring like element of the disc of radius r and thickness dr. If $σ$ is the surface charge density, then the charge on the element.
$d q = σ (r π r) d r$ ...(i)
Current di associated with rotating charge dq is
$d i = \frac{D q}{T} = \frac{d q ω}{2 π}$ ( $∴ T = \frac{2 π}{ω}$ ) ...(ii)

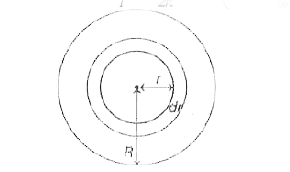
From Eqs. (i) and (ii), we get
$\Rightarrow d i = σ ω r d r$
As, the magnetic field dB at centre due to the element,
$d B = \frac{μ_{0} d i}{2 r} = \frac{μ_{0} σ ω r d r}{2 r} \Rightarrow d B = \frac{μ_{0} σ ω}{2} d r$
$\Rightarrow B_{net} = \frac{μ_{0} σ ω}{2} R \int 0 d r \Rightarrow B_{net} = \frac{μ_{0} σ ω R}{2}$
Hence, the correct option is (b).

Updated on:21/07/2023

|

Class 12 PHYSICS QUESTION PAPER 2019

Topper's Solved these Questions

Similar Questions

TS EAMCET PREVIOUS YEAR PAPERS-QUESTION PAPER 2019-Physics

Home
Ask Doubt
Profile