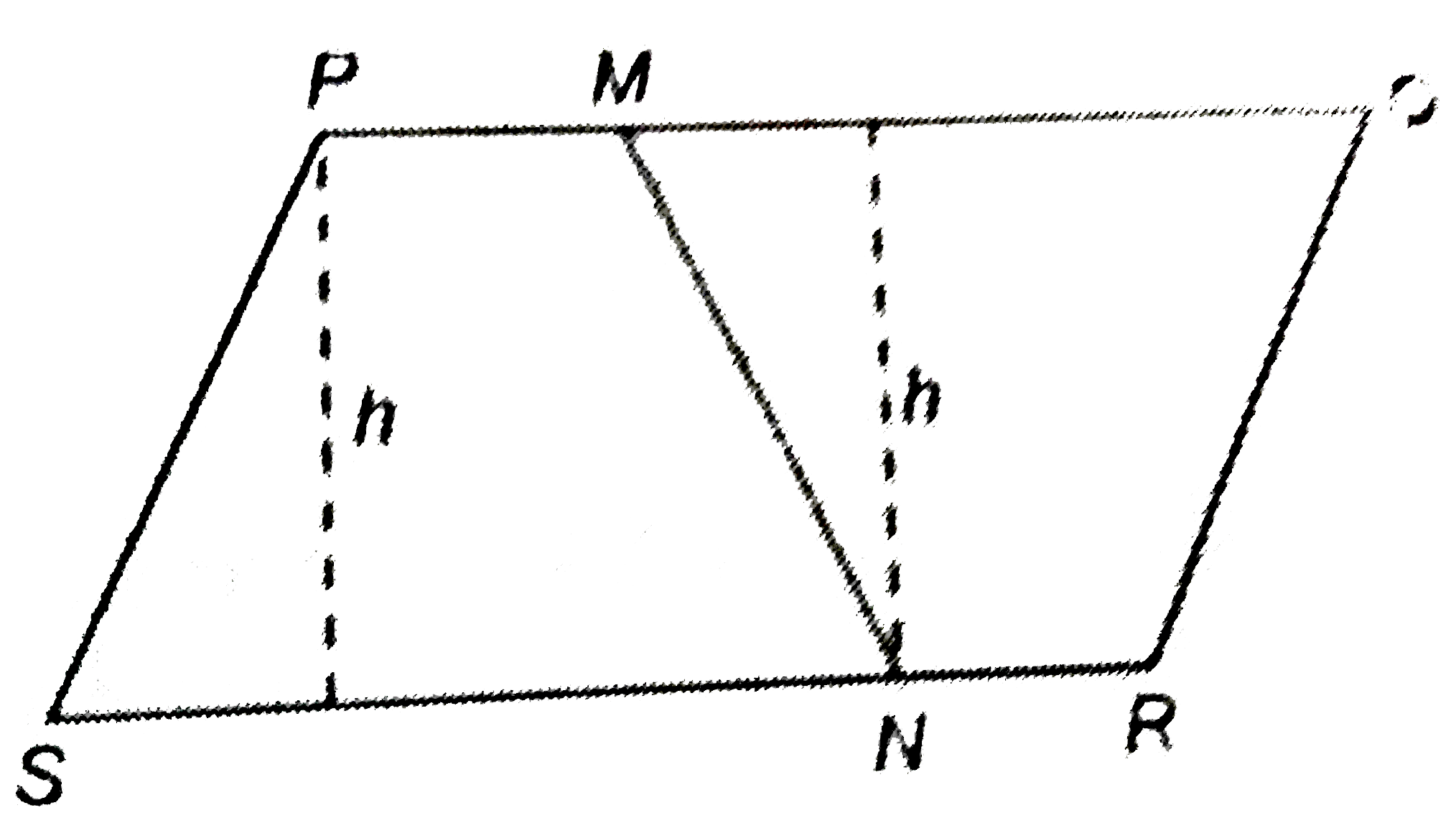
PQRS is a parallclogram such that PQ is parallel to SR and SP is parallel to RQ. The length of side PQ is 20 cm. M is point between P and Q such that the length of PM is 3 cm. N is a points between points S and R. Find the length of SN such that segment MN divides the parallelogram in two regions with equal areas.
15
17
16
18
The correct Answer is:B
Let h be the perpendicular distance between PQ and SR.
Since PQ = 20 cm and PM = 3 cm
∴MQ=20−3=17cm
Also, SR=PQ=20cm (becauseopposite sides of a parallelogram are equal)
Now, ar(Trap.PMNS)=ar(Trip.MQRN)(given)
⇒ 12×h(PM+SN)=12×h(MQ+NR)
⇒ 3+SN=17+(SR−SN)
⇒ 2.SN=17+20−3=34
= SN=17cm.
Topper's Solved these Questions
- QUADRILATERALSBOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Problems From NCERT/exemplar
11 Videos
- QUADRILATERALSBOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Exercise 8a
29 Videos
- PROBABILITYBOOK - NAGEEN PRAKASHANCHAPTER - PROBABILITYEXERCISE - Revision Exercise (very Short Answer /short Answer Questions)
10 Videos
- STATISTICSBOOK - NAGEEN PRAKASHANCHAPTER - STATISTICSEXERCISE - Revision Exercise
10 Videos
Similar Questions
Knowledge Check
PQRS is a parallclogram such that PQ is parallel to SR and SP is parallel to RQ. The length of side PQ is 20 cm. M is point between P and Q such that the length of PM is 3 cm. N is a points between points S and R. Find the length of SN such that segment MN divides the parallelogram in two regions with equal areas.
 A15B17C16D18
A15B17C16D18PQR is an equilateral triangle. MN is drawn parallel to QR such that M is on PQ and N is on PR. If PN = 6 cm, then the length of MN is
A3 cmB6 cmC12 cmD4.5 cmIn a circle of radius 10 cm, with centre O, PQ and PR are two chords each of length 12 cm. PO intersects chord QR at the points S. The length of OS is :
त्रिज्या 10 सेमी तथा केंद्र O वाले एक वृत्त में, PQ तथा PR दो जीवाएं हैं जिनमें से प्रत्येक की लंबाई 12 सेमी है | PO, जीवा QR को बिंदु S पर काटती है |OS की लंबाई है :A2.8 cm.B2.5 cm.C3.2 cm.D3 cm.
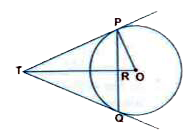
PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T . Find the length TP .
View SolutionPQ is a chord of length 8 cm, of a circle with centre O and of radius 5 cm. The tangents at P and Q intersect at a point T. The length of TP is
View SolutionDraw a line segment PQ = 10 cm. Take a points A on PQ such that PAPQ=25 Measure the length of PA and AQ
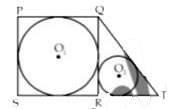
View SolutionIn the given figure, PQRS is a square of side 20 cm and SR is extended to point T. If the length of QT is 25 cm, then what is the distance (in cm) between the centres O1andO2 of the two circles?
View SolutionA tangent PQ at a point P of a circle of radius 5cm meets a line through the centre O at a point Q so that OQ=13cm. Find the length of PQ.
View Solution