A tangent PQ at a point P of a circle of radius 5cm meets a line through the centre O at a point Q so that OQ=13cm. Find the length of PQ.
12 cm
7 cm
10 cm
15 cm
The correct Answer is:A
To find the length of the tangent PQ from point P on the circle to point Q on the line through the center O, we can use the Pythagorean theorem. Here are the steps to solve the problem:
Step 1: Identify the given values
- Radius of the circle r=OP=5cm
- Length from the center to point Q OQ=13cm
Step 2: Set up the triangle
In triangle OPQ:
- OP is the radius of the circle (5 cm).
- OQ is the distance from the center to point Q (13 cm).
- PQ is the tangent we want to find.
Step 3: Apply the Pythagorean theorem
According to the Pythagorean theorem:
OQ2=OP2+PQ2
Substituting the known values:
132=52+PQ2
Calculating the squares:
169=25+PQ2
Step 4: Solve for PQ2
Rearranging the equation:
PQ2=169−25
PQ2=144
Step 5: Find PQ
Taking the square root of both sides:
PQ=√144=12cm
Thus, the length of the tangent PQ is 12cm.
Final Answer:
The length of PQ is 12cm.
---
- Radius of the circle r=OP=5cm
- Length from the center to point Q OQ=13cm
In triangle OPQ:
- OP is the radius of the circle (5 cm).
- OQ is the distance from the center to point Q (13 cm).
- PQ is the tangent we want to find.
According to the Pythagorean theorem:
OQ2=OP2+PQ2
Substituting the known values:
132=52+PQ2
Calculating the squares:
169=25+PQ2
Rearranging the equation:
PQ2=169−25
PQ2=144
Taking the square root of both sides:
PQ=√144=12cm
The length of PQ is 12cm.
Topper's Solved these Questions
- CIRCLESBOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Exercise 8A
16 Videos
- CIRCLESBOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Exercise 8B
15 Videos
- ARITHMETIC PROGRESSIONBOOK - RS AGGARWALCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Multiple Choice Questions (Mcq)
30 Videos
- CONSTRUCTIONSBOOK - RS AGGARWALCHAPTER - CONSTRUCTIONSEXERCISE - Test Yourself
10 Videos
Similar Questions
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ=13cm . Find the length of PQ .
View SolutionTangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Find length of PQ
View Solution
Knowledge Check
A tangent PQ at point P of a circle of radius 12 cm meets a line through the centre O to a point Q so that OQ = 20 cm . Length PQ is :
A14B15C16D10A tangent AB at a point A of a circle of radius 5 cm meets a line through the centre O at a point B so that OB = 12 cm , Length AB is
A10 cmB12 cmC9 cmD√119 cmA tangent AB, at a point A of a circle of radius 5 cm, meets a line through the centre O at point B such that OB =12 cm. Length AB is
A5 cmB12 cmC13 cmD√19 cm
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is:
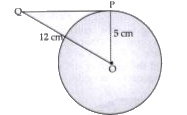
View SolutionA tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ =12 cm . Length PQ is :
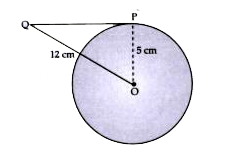
View SolutionA tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ=12 cm. Length PQ is :
(A) 12 cm (B) 13 cm (C) 8.5 cm (D) √119cm.
View SolutionA tangent PQ at a point P of a circle of radius 5cm meets a line through the centre O at a point Q such that OQ=12cm . Length PQ is (a) 12cm (b) 13cm (c) 8.5cm (d) √119cm
View SolutionIf the tangent at a point P to a circle with centre O cuts a line through O at Q such that PQ=24cm and OQ=25cm . Find the radius of the circle.
View Solution
