The radii of the two columne is U-tube are $r_{1}$ and $r_{2} (> r_{1})$ . When a liquid of density $ρ$ (angle of contact is $0^{\circ}))$ is filled in it, the level different of liquid in two arms is h. The surface tension of liquid is
$(g =$ acceleration due to gravity)

A

$\frac{ρ g h r_{1} r_{2}}{2 (r_{2} - r_{1})}$

B

$\frac{ρ g h (r_{1} - r_{2})}{2 r_{1} r_{2}}$

C

$\frac{2 (r_{2} - r_{1})}{ρ g h r_{1} r_{2}}$

D

$\frac{ρ g h}{2 (r_{2} - r_{1})}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Let $h_{1}, h_{2}$ be the heights to which liquid rises in two columns of radii $r_{1}$ and $r_{2}$ respectively. Then
$h_{1} = \frac{2 S {cos O}^{\circ}}{r_{1} ρ g} = \frac{2 S}{r_{1} ρ g}$
Where s is the surface tension of liquid.
and $h_{2} = \frac{2 S {cos o}^{\circ}}{r_{2} ρ g} = \frac{2 S}{r_{2} ρ g}$
$∴$ Difference in levels of liquid in two arms of U tube is
$h = h_{1} - h_{2} = \frac{2 S}{ρ g} [\frac{1}{r_{2}} - \frac{1}{r_{2}}] = 2 S \frac{(r_{2} - r_{1})}{r_{1} r_{2} ρ g}$
$S = \frac{r_{1} r_{2} ρ g h}{2 (r_{2} - r_{1})}$

|

Updated on:21/07/2023

Class 11 PHYSICS PROPERTIES OF SOLIDS AND FLUIDS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One

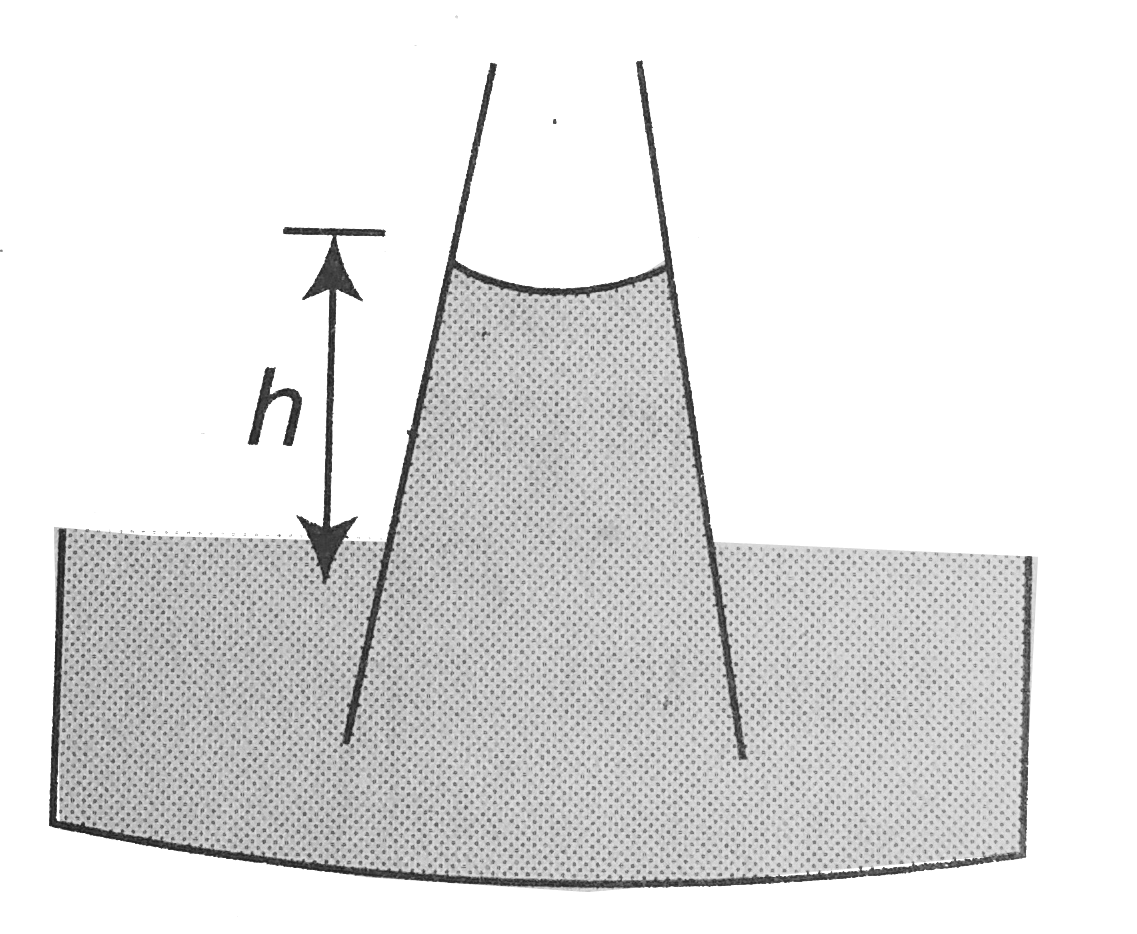
A capillary of the shape as shown is dipped in a liquid. Contact angle between the liquid and the capillary is $0^{\circ}$ and effect of liquid inside the mexiscus is to be neglected. $T$ is surface tension of the liquid, $r$ is radius of the meniscus, $g$ is acceleration due to gravity and $ρ$ is density of the liquid then height $h$ in equilibrium is:
Agreater than $\frac{2 T}{r ρ g}$
Bequal to $\frac{2 T}{r ρ g}$
Cless than $\frac{2 T}{r ρ g}$
Dof any value depending upon act.
Question 2 - Select One
A beaker containing a liquid of density $ρ$ moves up with an acceleration $a$ . The pressure due to the liquid at a depth h below the free surface of the liquid is.
A $h ρ g$
B $h ρ (g + a)$
C $h ρ (g - a)$
D $2 h ρ g (\frac{g - a}{g + a})$
Question 3 - Select One
If h is the rise of water in a capillary tube of radius r, then the work done by the force of surface tension is
$(ρ$ is density g = ${(acc)}^{n}$ due to gravity )
A $\frac{2 g T^{2}}{ρ π}$
B $\frac{2 π T^{2}}{ρ g}$
C $\frac{4 g T^{2}}{ρ π}$
D $\frac{4 π T^{2}}{ρ g}$

NCERT FINGERTIPS-MECHANICAL PROPERTIES OF FLUIDS-Surface Tension

Home
Ask Doubt
Profile