Two blocks of masses and are connected by a metal wire going over a smooth pulley as shown in figure.
The breaking stress of the metal is . If , then what should be the minimum radius of the wire used if it is not to break?

0.5 mm
1 mm
1.5 mm
2 mm
The correct Answer is:B
If r is the minimum radius, then
Breaking stress
or
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTIPSCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - NCERT Exemplar
8 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTIPSCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assertion And Reason
15 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTIPSCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Applications Of Elastic Behaviour Of Materials
8 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NCERT FINGERTIPSCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Assertion And Reason
15 Videos
- MOTION IN A PLANE BOOK - NCERT FINGERTIPSCHAPTER - MOTION IN A PLANE EXERCISE - Assertion And Reason
15 Videos
Similar Questions
Two blocks of masses 1 kg and 2kg are connect by a metal wire going over a smooth pulley as shown in figure. The breaking stress of the metal is 2×109m−2. What should be the minmum radius of the wire used if it is not to break? Take g=10ms−2
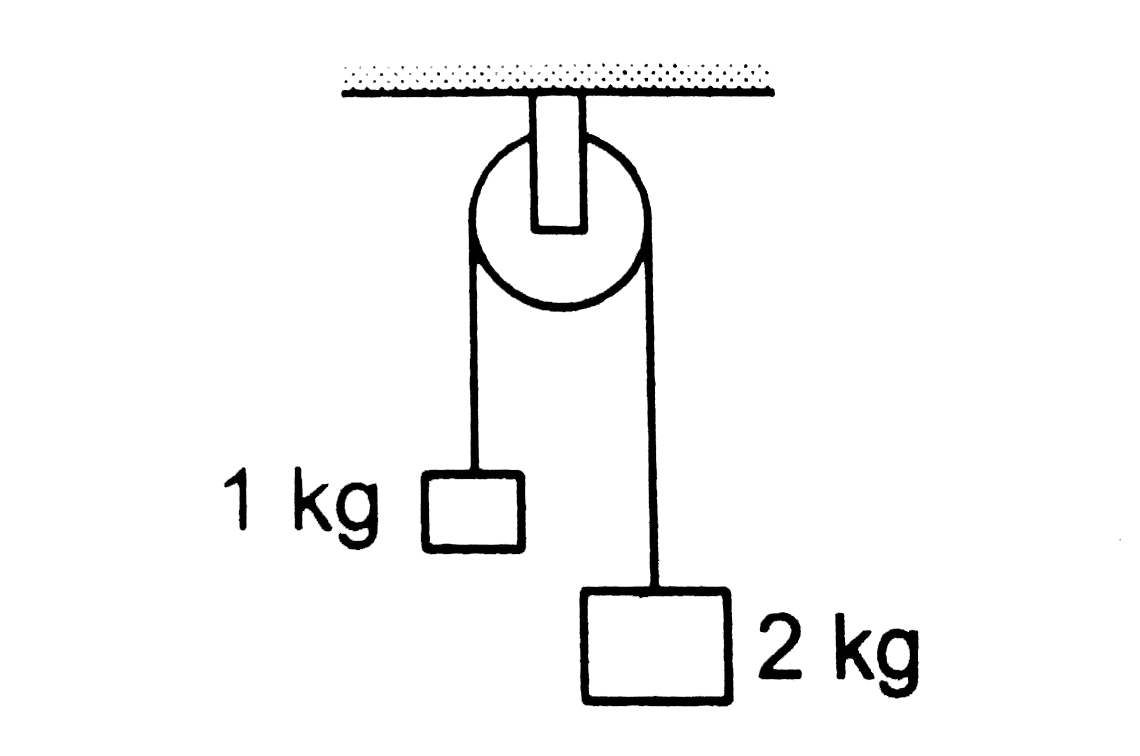
View SolutionTwo blocks of masses 2 kg and 3kg are connected by a metal wire going over a smoother pulley as shown in figure. The breaking stress of the steel is 2×109Nm−2. What would be the minimum radius of the wire used if it not to break ? Take ,g=10ms−2
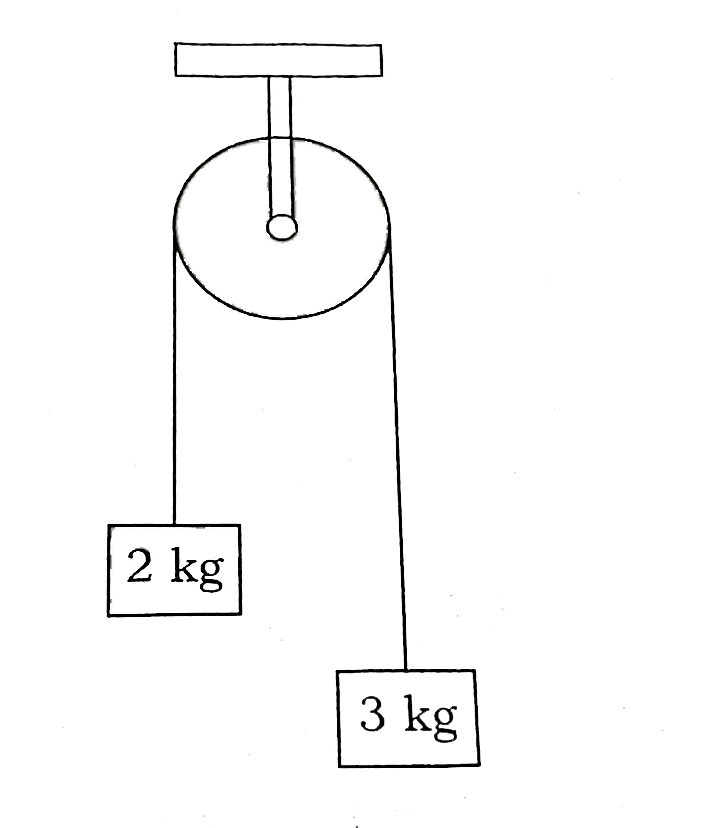
View Solution
Knowledge Check
Two blocks of masses 1kg and 2kg are connected by a metal wire goijng over a smooth pulley as shown in figure.
The breaking stress of the metal is (40/3π)×106N/m2. If g=10ms−12, then what should be the minimum radlus of the wire used if it is not to break?
 A0.5mmB1mmC1.5mmD2mm
A0.5mmB1mmC1.5mmD2mmTwo blocks of masses 5 kg and 10 kg are connected by a metal wire going over a smooth pulley as shown in the figure. The breaking stress of the metal wire is 2×109N m−2. If g=10ms−2, then what is the minimum radius of the wire which will not break
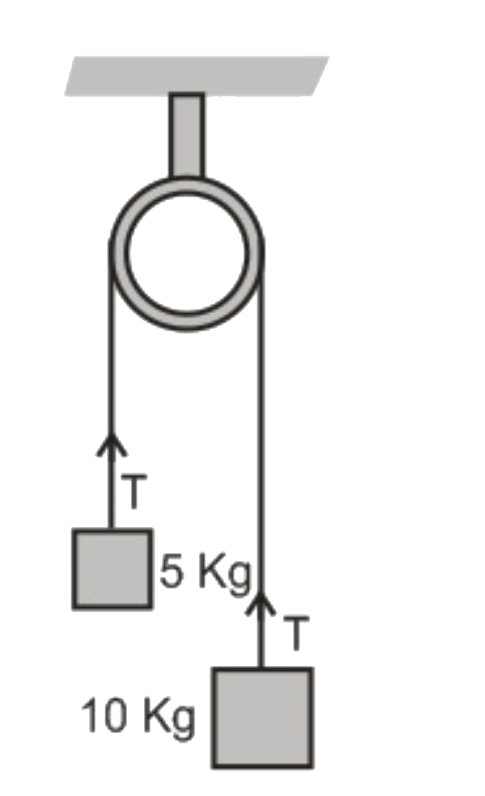 A0.1 mmB0.2 mmC0.05 mmD0.25 mm
A0.1 mmB0.2 mmC0.05 mmD0.25 mmTwo blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
Two blocks of masses 3 kg and 5 kg are connected by a metal wire going over a smooth pulley. The breaking stress of the metal is 24π×102Nm−2 . What is the minimum radius of the wire ?
(take g=10ms−2)
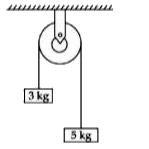
View SolutionTwo masses of 10 kg and 20 kg are connected with an inextensible string passing over two smooth pulleys as shown in the figure. The acceleration of 20 kg mass will be :
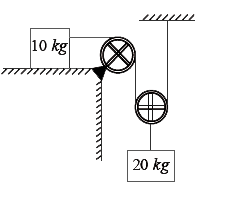
View SolutionTwo blocks of masses 3 kg and 6 kg are connected by a string as shown in the figure over a frictionless pulley. The acceleration of the system is

View SolutionTwo blocks A and B , each of mass 10kg , are connected by a light string passing over a smooth pulley as shown in the figure. Block A will remain at rest if the friction on it is

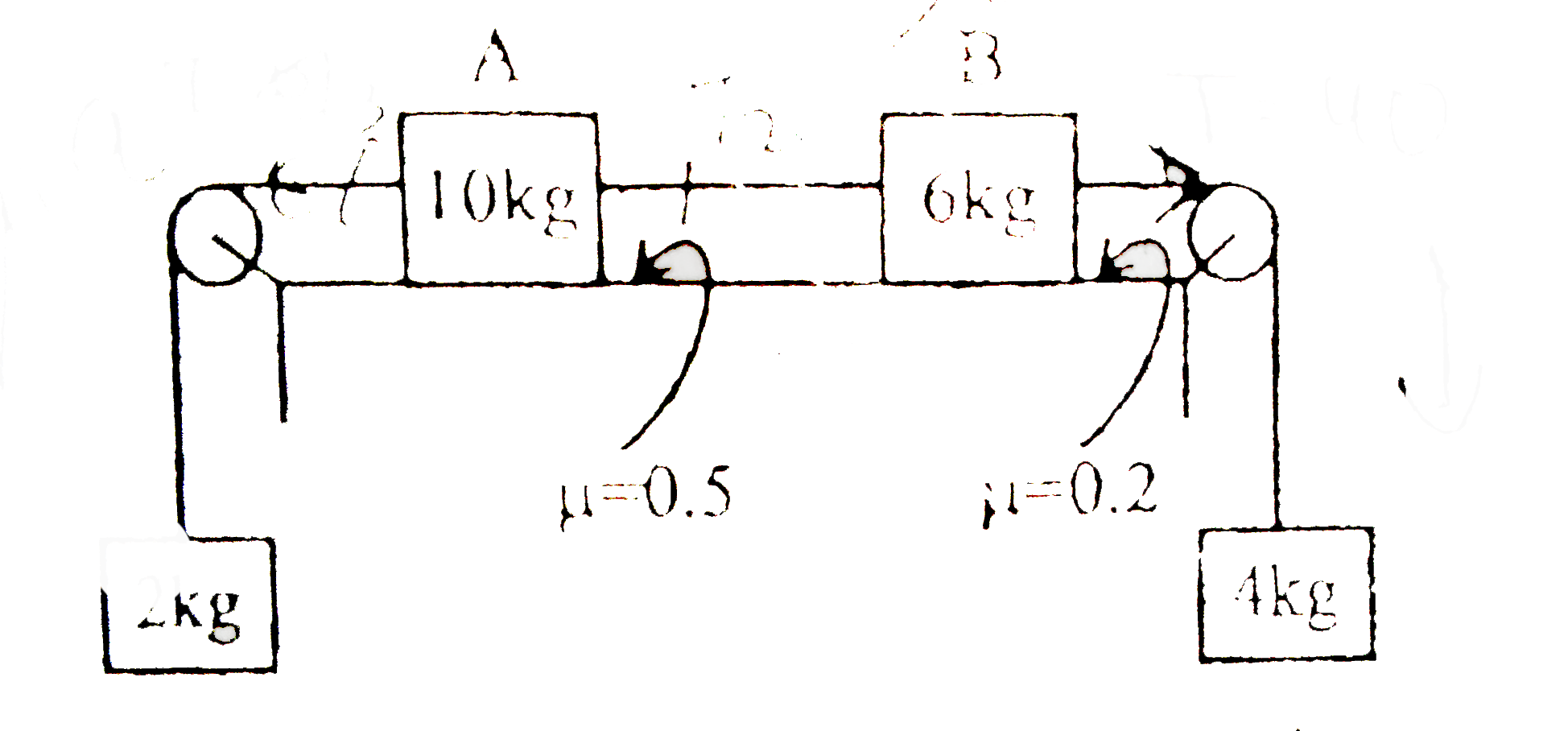
View SolutionTwo Block A and B of masses 10kg and 6kg respectively are connected through pulley as shown in figure. Find acceleration of block A.
View Solution
