Two opposite forcesF1=120N and F2=80N act on an elastic plank of modulus of elasticity Y=2x1011N/m2 and length l=1m placed over a smooth horizontal surface. The cross-sectional area of the plank is S=0.5m2. The change in length of the plank is x×10−11m. Find the value of x.

1
1.5
1.4
1.1
The correct Answer is:A
Consider an element of thickness dx, Change in the length of the element is dl=TSdxY and T=F1−(F1−F2)xl
Δl∫0dll∫0F1−(F1−F2)dxldxSY
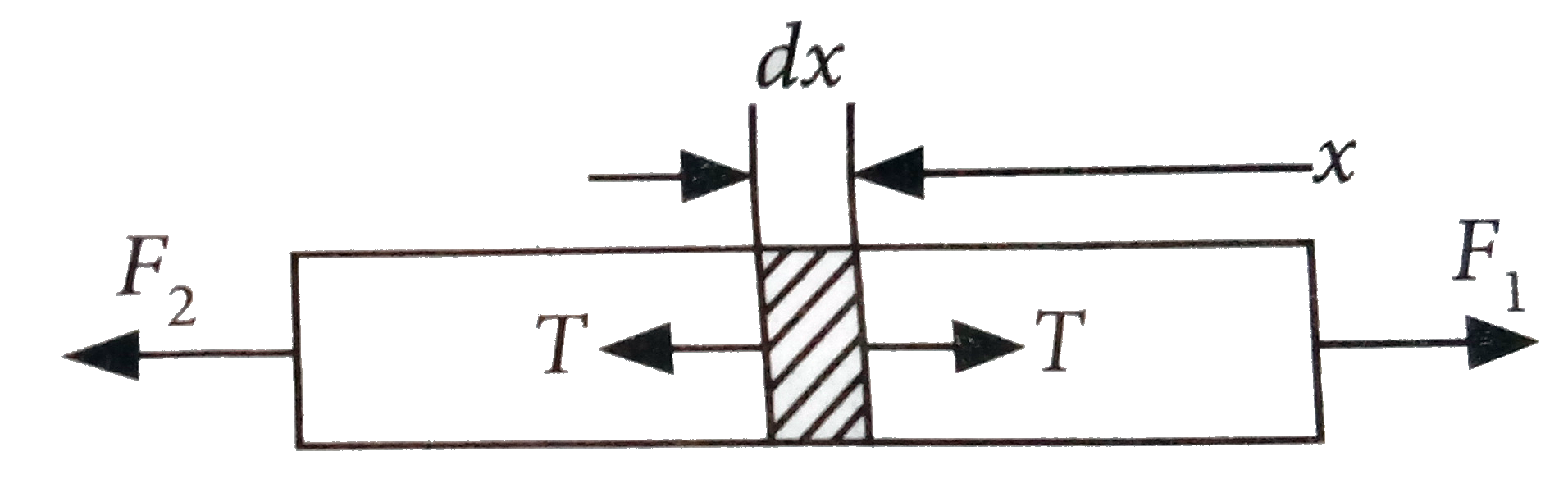
Δl=(F1+F2)2SY=200×12×0.5×2×1011=1×10−9m
∴x=1
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTIPSCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - NCERT Exemplar
8 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTIPSCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assertion And Reason
15 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTIPSCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Applications Of Elastic Behaviour Of Materials
8 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NCERT FINGERTIPSCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Assertion And Reason
15 Videos
- MOTION IN A PLANE BOOK - NCERT FINGERTIPSCHAPTER - MOTION IN A PLANE EXERCISE - Assertion And Reason
15 Videos
Similar Questions
Young modulus of elasticity of brass is 1011N/m2. On pressing the rod of length 0.1 m. and cross section area 1cm2 made from brass with a force of 10 N. along its length, the increase in its energy will be……………………
View SolutionIf m and n are the zeros of the polynomial 3x2+11x−4, find the value of mn+nm.
View Solution
Knowledge Check
A uniform plank of Young's modulus Y is moved over a smooth horizontal surface by a constant horizontal force F. The area of cross section of the plank is A. The compressive strain on the plank in the direction of the force is
AF/AYB2F/AYC12(F/AY)D3F/AYIf young's modulus of steel is 2×1011N/m2, then the force required to increase the length of a wire of cross section 1cm2 by 1% will be
A105NB2×105NC104ND2×104NThe area of a cross-section of steel wire is 0.5cm−2 and Young's modulus of steel is 2×1011Nm−2. The force required to stretch by 0.5% of its length is
A1000 NB2000 NC4000 ND5000N
A wire of length 1m is stretched by a force of 10N. The area of cross-section of the wire is 2×10–6m2 and Y is 2×1011N/m2 . Increase in length of the wire will be -
View SolutionA sphere of mass m and radius r is placed on a rough plank of mass M. The system is placed on a smooth horizontal surface. A constant force F is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.

View SolutionA block of mass'm' it kept over the smooth surface of the plank of mass M. the plank of length l is kept over the smooth horizontal surface. A constant horizontal force F is applied onto the plank as shown in figure. Calculate the time after which the block falls off the plank?

View SolutionA 20 N stone is suspended from a wire and its length changes by 1%. If the Young's modulus of the material of wire is 2×1011N/m2, then the area of cross-section of the wire is 2×1011N/m2, then the area of cross-section of the wire will be
View SolutionWhen a force is applied on a wire of uniform cross-sectional area 3×10−6m2 and length 4 m, the increase in length is 1mm. Energy stored in it will be (Y=2×1011N/m2)
View Solution
