The intial velocity of a particle moving along x axis is u (at t = 0 and x = 0) and its acceleration a is given by a = kx. Which of the following equation is correct between its velocity (v) and position (x)?
v2=y2=2kx
v2=u2+2kx2
v2=u2+kx2
v2+u2=2kx
The correct Answer is:C
To solve the problem, we need to derive the relationship between the velocity v and the position x of a particle given that its acceleration a is proportional to its position x, specifically a=kx.
1. Understand the Given Information:
- Initial velocity u at t=0 and x=0.
- Acceleration a=kx.
2. Relate Acceleration to Velocity and Position:
- We know that acceleration can be expressed in two ways:
a=dvdt(1)
and
a=vdvdx(2)
- Since both expressions represent acceleration, we can set them equal to each other:
dvdt=vdvdx
3. Substituting the Expression for Acceleration:
- From the problem, we have a=kx. Therefore, we can substitute a in equation (1):
kx=vdvdx
4. Rearranging the Equation:
- Rearranging gives:
vdv=kxdx
5. Integrating Both Sides:
- Now we integrate both sides. The left side integrates from u to v and the right side from 0 to x:
∫vuvdv=∫x0kxdx
6. Calculating the Integrals:
- The left-hand side:
v22∣∣∣vu=v22−u22
- The right-hand side:
k∫x0xdx=k(x22)∣∣∣x0=kx22
7. Setting the Two Integrals Equal:
- Now we equate both results:
v22−u22=kx22
8. Simplifying the Equation:
- Multiply through by 2 to eliminate the fractions:
v2−u2=kx2
- Rearranging gives:
v2=u2+kx2
Final Result:
The correct relationship between the velocity v and the position x is:
v2=u2+kx2
- Initial velocity u at t=0 and x=0.
- Acceleration a=kx.
- We know that acceleration can be expressed in two ways:
a=dvdt(1)
and
a=vdvdx(2)
- Since both expressions represent acceleration, we can set them equal to each other:
dvdt=vdvdx
- From the problem, we have a=kx. Therefore, we can substitute a in equation (1):
kx=vdvdx
- Rearranging gives:
vdv=kxdx
- Now we integrate both sides. The left side integrates from u to v and the right side from 0 to x:
∫vuvdv=∫x0kxdx
- The left-hand side:
v22∣∣∣vu=v22−u22
- The right-hand side:
k∫x0xdx=k(x22)∣∣∣x0=kx22
- Now we equate both results:
v22−u22=kx22
- Multiply through by 2 to eliminate the fractions:
v2−u2=kx2
- Rearranging gives:
v2=u2+kx2
The correct relationship between the velocity v and the position x is:
v2=u2+kx2
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBook:AAKASH INSTITUTEChapter:MOTION IN A STRAIGHT LINEExercise:ASSIGNMENT (SECTION - C)
Explore 37 Videos
- MOTION IN A STRAIGHT LINEBook:AAKASH INSTITUTEChapter:MOTION IN A STRAIGHT LINEExercise:ASSIGNMENT (SECTION - D)
Explore 15 Videos
- MOTION IN A STRAIGHT LINEBook:AAKASH INSTITUTEChapter:MOTION IN A STRAIGHT LINEExercise:ASSIGNMENT (SECTION - A)
Explore 60 Videos
- MOTION IN A PLANEBook:AAKASH INSTITUTEChapter:MOTION IN A PLANEExercise:Assignement section -J (Aakash Challengers Questions)
Explore 4 Videos
- MOTION IN STRAIGHT LINEBook:AAKASH INSTITUTEChapter:MOTION IN STRAIGHT LINEExercise:Assignment (SECTION - J)
Explore 2 Videos
Similar Questions
Knowledge Check
The intial velocity of a particle is u (at t=0) and the acceleration is given by f=at. Which of the following relations is valid ?
Av=u+at2Bv=u+at22Cv=u+atDv=uThe position of a particle moving along x- axis is given by x=x0cos2(ωt) . Its when it is at mean position is
A2x0ωBx0ω2Cx0ω2Dx0ωThe velocity v of a particle moving along x - axis varies with ist position (x) as v=α√x, where α is a constant. Which of the following graph represents the variation of its acceleration (a) with time (t)?
A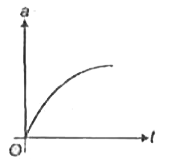 B
B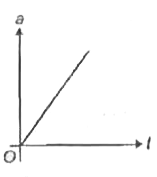 C
C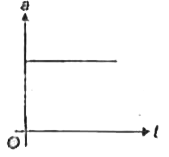 D
D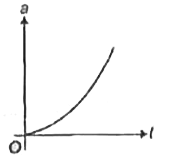
The velocity of a particle is v=v_(0)+gt+ft^(2) .If its position is x=0 at t=0, then its displacement after 1s is
View SolutionIf the velocity of the a particle moving on x-axis is given by v=3t2−12t+6. at what time is the acceleration of particle zero ?
View SolutionThe velocity (υ) of a particle moving along X-axis varies with its position x as shown in figure. The acceleration (a) of particle varies with position (x) as
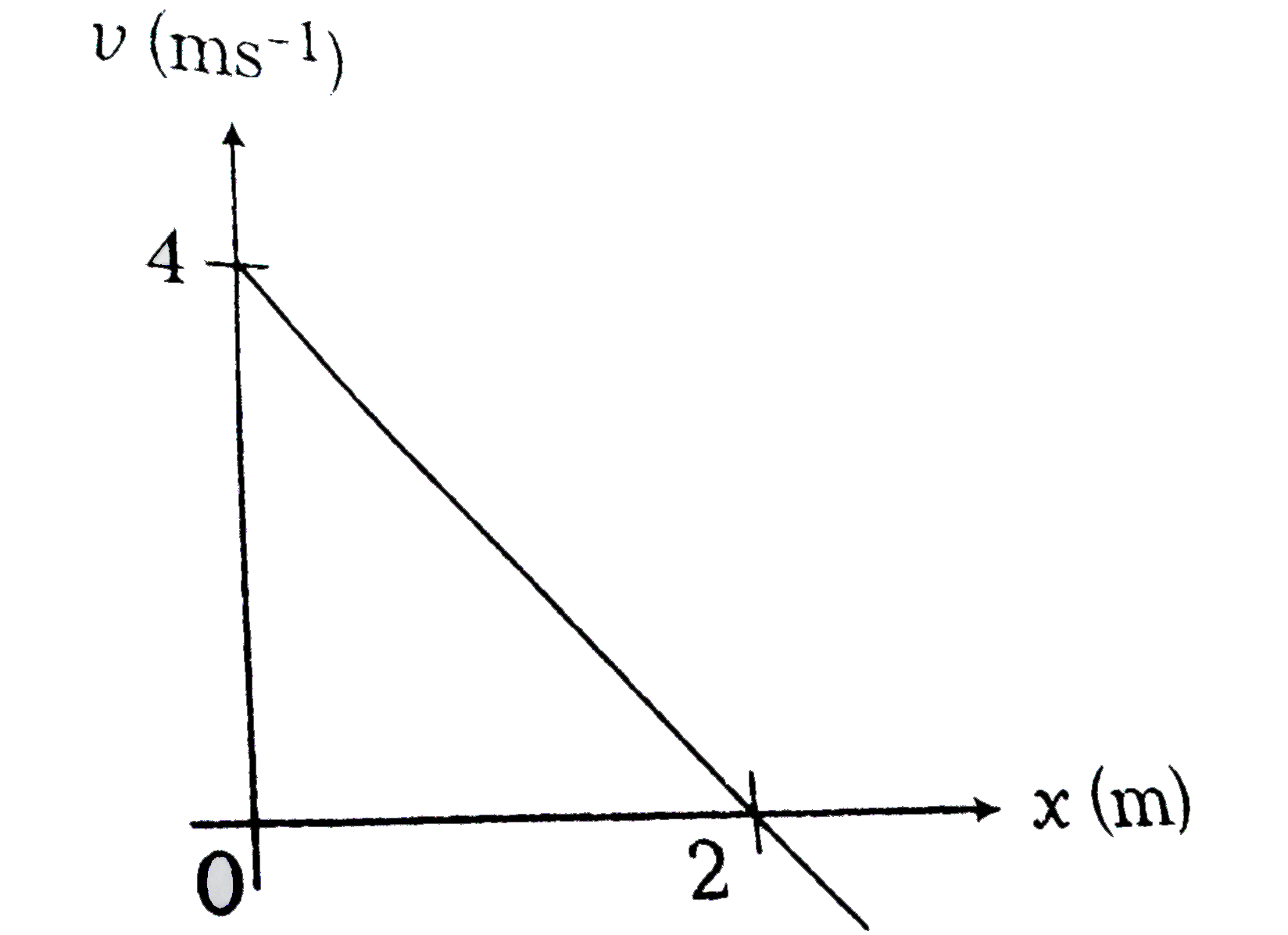
View SolutionA particle is moving along the x-axis with an acceleration a = 2x where a is in ms–2andx is in metre. If the particle starts from rest at x=1 m, find its velocity when it reaches the position x = 3.
View Solutionvx is the velocity of a particle moving along the x-axis as shown in the figure. If x=2.0m at t=1.0s, what is the position of the particle at t=6.0s ?
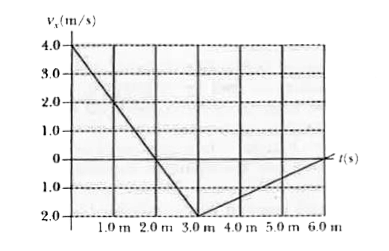
View Solution

