Suppose Q is a point on the circle with center P and radius 1, as shown in the figure , R is a point outside the circle such that QR=1and∠QRP=2∘ . Let S be the point where the segment RP intersects the given circle. Then measure of ∠RQS equals-
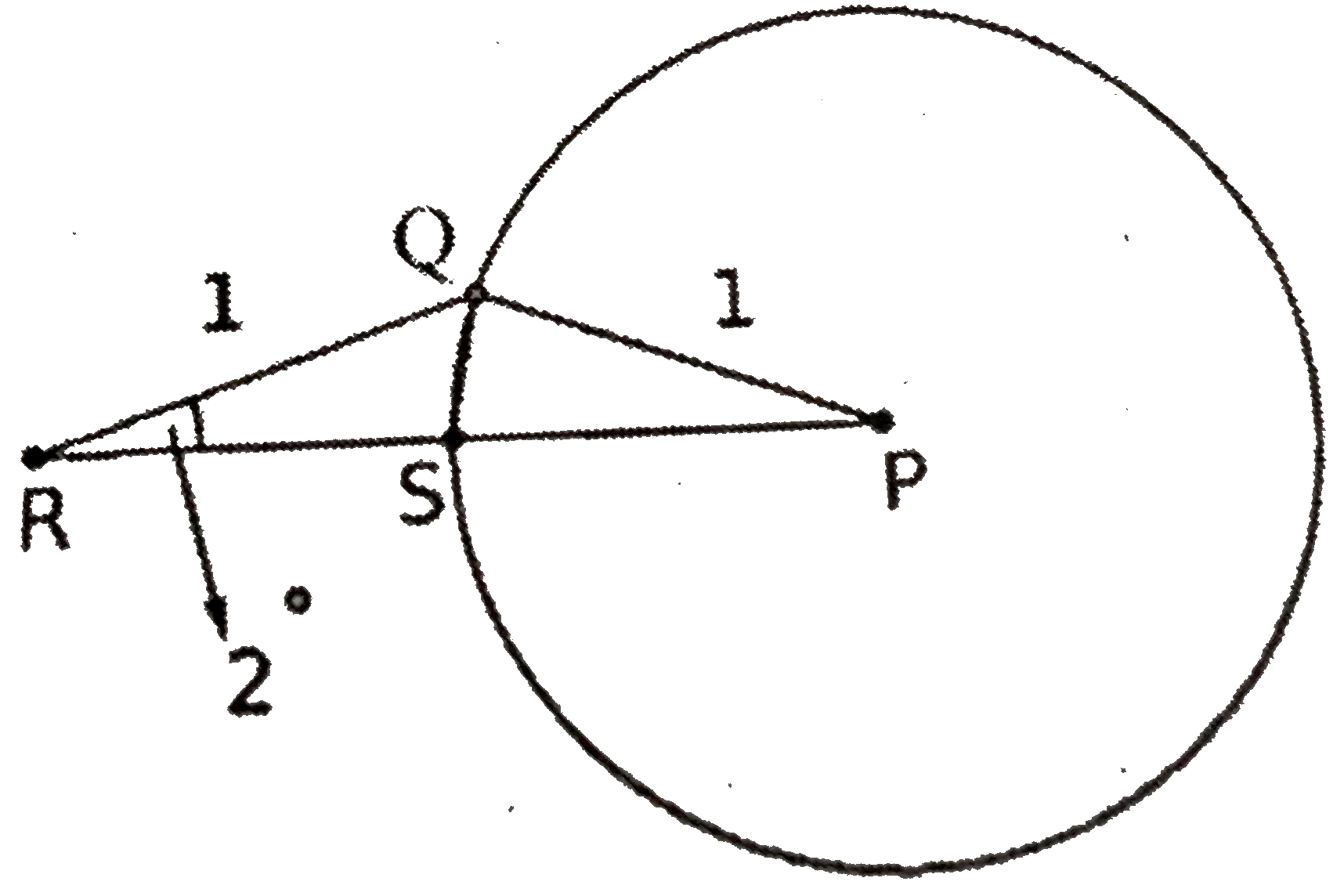
86∘
87∘
88∘
89∘
The correct Answer is:D
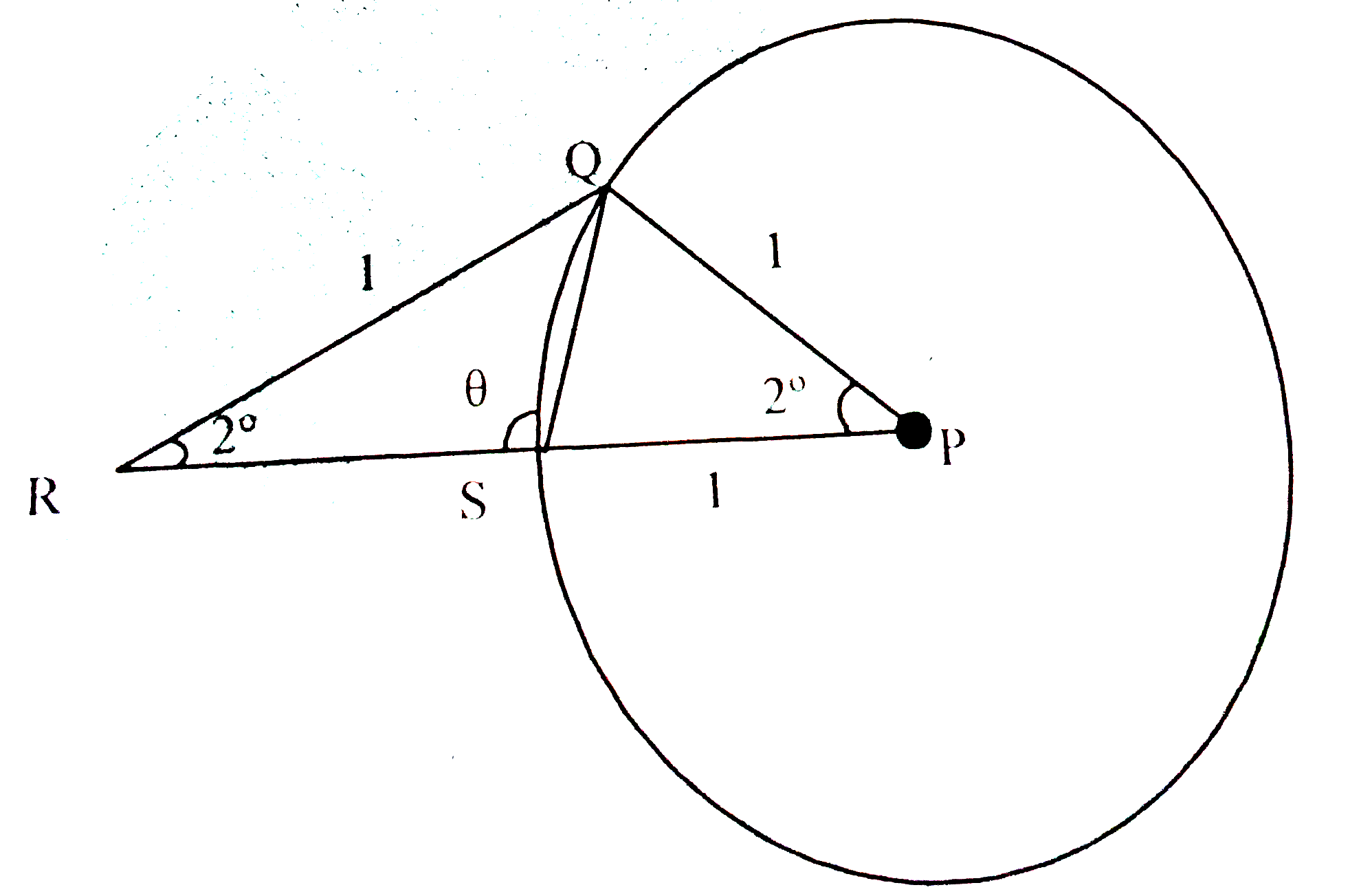
By Cosine rule
(QS)2=2−2cos2∘
QS=2sin1∘
Now by sine rule in ΔRQS
sinθ=sin2∘2sin1∘
θ=89∘
∠RQS=180∘−(2+89∘)=180∘−91∘=89∘
Topper's Solved these Questions
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - PART-2 MATHEMATICS
5 Videos
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - PART-2(MATHEMATICS)
10 Videos
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - exercise
18 Videos
- KVPY 2021BOOK - KVPY PREVIOUS YEARCHAPTER - KVPY 2021EXERCISE - PART II MATHEMATICS
4 Videos
Similar Questions
Suppose Q is a point on the circle with centre P and radius 1, as shown in the figure: R is a point outside the circle such that QR=1 and ∠QRP=2∘. Let S be the point where the segment RP intersects the given circle. Then measurement of ∠RQS equals
View SolutionA circle has its centre at the origin and a point P (5,0) lies on it . The point Q (6,8) lies outside the circle.
View Solution
Knowledge Check
PA and PB are two tangents to a circle with centre O, from a point P outside the circle. A and B are points on the circle. If ∠APB=100∘ , then OAB is equal to:
A25∘B20∘C35∘D50∘PA and PB are tangents to a circle with centre 0, from a point P outside the circle, and A and B are point on the circle. If ∠APB=30∘, then ∠OAB is equal to:
A25∘B40∘C15∘D50∘P is a point outside a circle with centre O, and it is 14 cm away from the centre. A secant PAB drawn from P intersects the circle at the points A and B such that PA = 10 cm and PB = 16 cm. The diameter of the Circle is:
A10 cmB13 cmC12 cmD11 cm
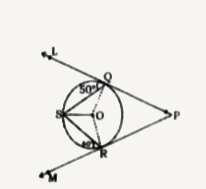
In the given figure, PQL and PRM are tangents to the circle with centre 'O' at the points Q and R, respectively and S is a point on the circle such that ∠SQL=50∘and∠SRM=60∘. Then ∠QSR is equal to
View SolutionLet P be a point on the circle S with both coordinates being positive. Let the tangent to S at P intersect the coordinate axes at the points M and N. Then, the mid-point of the line segment MN must lie on the curve.
View SolutionPA and PB are two tangents to a circle with centre 0. from a point P outside the circle. A and B are points on the circle. If ∠APB=70∘ then ∠OAB is equal to:
View SolutionThe tangent at a point A on a circle with center O intersects the diameter PQ of the circle, when extended,at point B. If ∠BAQ=105∘, then ∠APQ is equal to:
View SolutionTangents to a circle at points P and Q on the circle intersect at a point R. If PQ= 6 and PR= 5 then the radius of the circle is
View Solution