A circle has its centre at the origin and a point P (5,0) lies on it . The point Q (6,8) lies outside the circle.
The correct Answer is:1
First , we draw a circle and a point from the given information.

Now , distance between origin i.e., O(0,0) and P (5,0), OP =√(5−0)2+(0−0)2
[∵ Distance between two points (x1,y1)and(x2,y2),d=√(x2−x1)2+(y2−y1)2]
=√52+02=5= Radius of circle and distance between origin O(0,0)
and Q(6,8),OQ=√(6−0)2+(8−0)2=√62+82=√36+64=√100=10
We know that , if the distance of any point from the centre is less than/ equal to/more than the radius , then the point is inside/on/outside the circle, respectively.
Here , we see that , OQ<OP
Hence , it is true that point Q (6,8) , lies outside the circle.
Topper's Solved these Questions
- CONSTRUCTIONSBOOK - NCERT EXEMPLARCHAPTER - CONSTRUCTIONSEXERCISE - Exercise 10.4 Long Answer type Questions
7 Videos
- INTRODUCTION TO TRIGoNOMETRY AND ITS APPLICATIONSBOOK - NCERT EXEMPLARCHAPTER - INTRODUCTION TO TRIGoNOMETRY AND ITS APPLICATIONSEXERCISE - Introduction To Trigonometry And Its Applications
60 Videos
Similar Questions
Knowledge Check
The point (5,−7) lies outside the circle
Ax2+y2−8x=0Bx2+y2−5x+7y=0Cx2+y2−5x+7y−1=0Dx2+Y2−8x+7y−2=0Point (0,−8) lies
Ain the II quadrantBin the IV quadrantCon the x-axisDon the y-axisThe centre of the circle is at the origin and its radius is 10. Which of the following points lies inside the circle?
A(6,8)B(0, 11)C(-10,0)D(7,7)
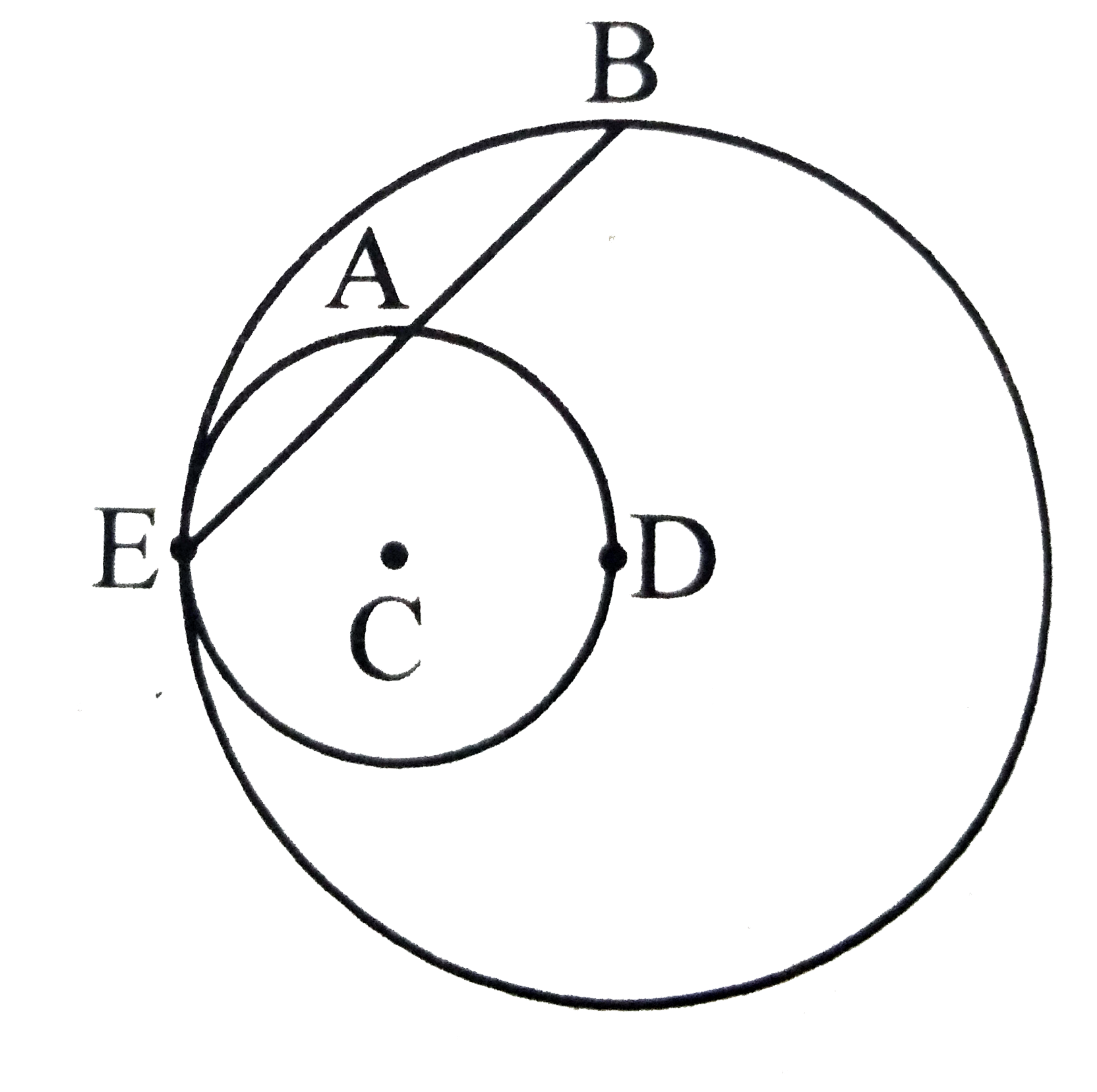
In the adjoining figure , circles with centres C and D touch internally at point E. D lies on the inner circle. Chord EB of the other circle intersects innet circle at point A. Prove that, seg EA≅seg AB.
View SolutionThe point (-a, - a) lies on the circle passing through the origin and the point of intersection of the straight line x+y+a=0 with the circle x2+y2=a2
View SolutionIn the xy plane, the segment with end points (3,8) and (-5,2) is the diameter of the circle. The point (k,10) lies on the circle for
View SolutionPA and PB are two tangents to a circle with centre O, from a point P outside the circle . A and B are point P outside the circle . A and B are point on the circle . If ∠PAB=47∘ , then ∠OAB is equal to :
View SolutionIf 3x+y=0 is a tangent to a circle whose center is (2,−1) , then find the equation of the other tangent to the circle from the origin.
View Solution
