Question

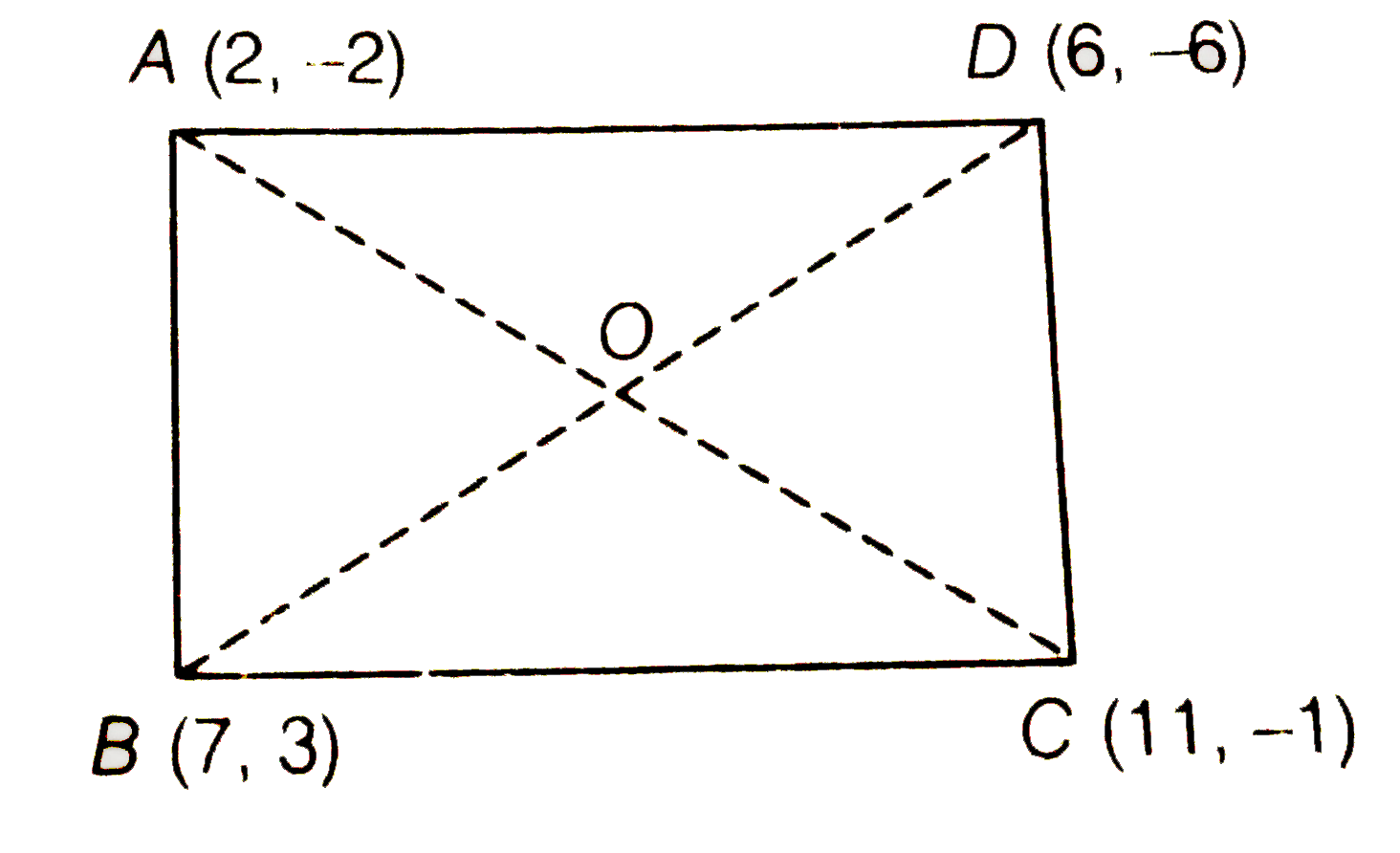
What type of quadrilateral do the points $A(2,-2),B(7,3),C(11,-1)\text{and}D(6,-6)$ taken in that order form?

Explanation

To find the type of quadrilateral , we find the length of all four sides as well as two diagonals and see whatever condition of quandrilateral is satisfy by these sides as well as diagonals. Now , using distance formula between two points,
sides , AB `= sqrt((7-2)^(2)+(3+2)^(2))`
`=sqrt((5)^(2)+(5)^(2))=sqrt(25+25)`
`=sqrt(50)=5sqrt(2)`
[since , distance between two points `(x_(1),y_(1))and(x_(2),y_(2))=sqrt((x_(2)-x_(1))+(y_(2)-y_(1))^(2))]`
BC `=sqrt((11-7)^(2)+(-1-3)^(2))=sqrt((4)^(2)+(-4)^(2))`
`=sqrt(16+16)=sqrt(32)=4sqrt(2)`
CD `=sqrt((16-11)^(2)+(-6+1)^(2))`
`=sqrt((-5)^(2)+(-5)^(2))`
`=sqrt(25+25)=sqrt(50)=5sqrt(2)`
and DA `=sqrt((2-6)^(2)+(-2+6)^(2))`
`=sqrt((-4)^(2)+(4)^(2))=sqrt(16+16)`
`=sqrt(32)=4sqrt(2)`
Diagonals , AC `=sqrt((11-2)^(2)+(-1+2)^(2))`
`=sqrt((9)^(2)+(1)^(2))=sqrt(81+1)=sqrt(82)`
and BD `=sqrt((6-7)^(2)+(-6-3)^(2))`
`=sqrt((-1)^(2)+(-9)^(2))`
`=sqrt(1+81)=sqrt(82)`
Here , we see that the sides AB=CD and BC =DA
Also , diagonals are equal i.e., AC=BD
which shown the quadrilateral is a reactangle.