The tangent at a point A on a circle with center O intersects the diameter PQ of the circle, when extended,at point B. If ∠BAQ=105∘, then ∠APQ is equal to:
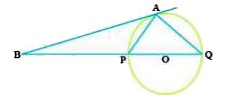
55∘
60∘
65∘
75∘
The correct Answer is:D
Step by step video, text & image solution for The tangent at a point A on a circle with center O intersects the diameter PQ of the circle, when extended,at point B. If angleBAQ=105^(@), then angleAPQ is equal to: by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Similar Questions
The tangent at a point A of a circle with centre O intersects the diameter PQ of the circle (when extended) at the point B. If ∠BAP=125∘, then ∠AQP is equal to:
केंद्र O के साथ एक वृत्त के बिंदु A पर स्पश्रेखा, बिंदु , B पर वृत्त के व्यास PQ ( जब विस्तारित) को काटती है यदि∠BAP=125∘ है, तो ∠AQP के ज्ञात करें ।
View SolutionIn figure-3, PQ is tangent to the circle with centre at O, at the point B. if ∠AOB=100∘, then ∠ABP is equal to
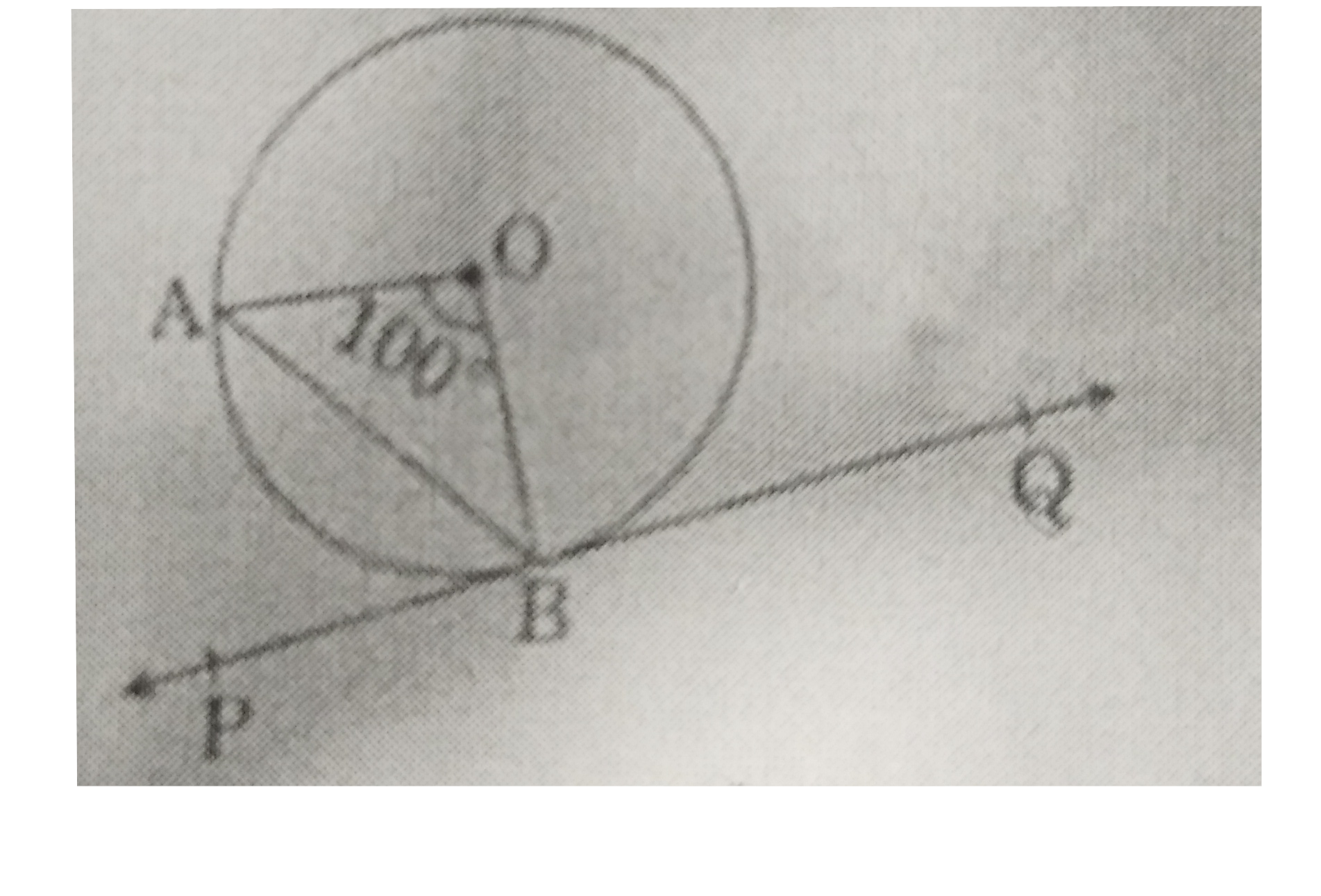
View Solution
Knowledge Check
The tangent at a point A of a circle with centre O intersects the diameter PQ of the circle (when extended) at the point B. If ∠BAP=125∘, then ∠AQP is equal to :
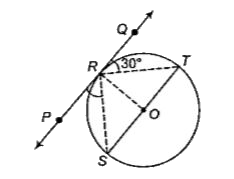
A45∘B55∘C60∘D50∘PQ is tangent at a point R of the circle with centre O. If ST is a diameter of the circle and ∠TRQ=30∘ find ∠PRS
A30∘B60∘C45∘D120∘PA and PB are two tangents to a circle with centre O, from a point P outside the circle. A and B are points on the circle. If ∠APB=100∘ , then OAB is equal to:
A25∘B20∘C35∘D50∘
In figure PQ is tangent to the circle with centre at O at the point B , if ∠AOB=100∘, then ∠ABP is equal to

View SolutionPQ is a tangent drawn from an external point P to a circle with center O, ∠QOR is the diameter of the circle. If ∠POR=120∘. What is the measure of ∠OPQ?
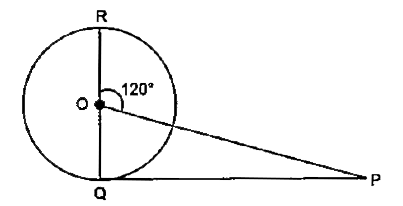
View SolutionIn the given figure, PQ is a tangent at a point R of the circle with centre O. If ∠TRQ=30∘, then ∠PRS is equal to
View SolutionPA and PB are tangents to a circle with centre O, from a point P outside the circle and A and B are points on the circle. If ∠APB=30∘, then ∠OAB is equal to :
View SolutionPA and PB are two tangents to a circle with centre O, from a point P outside the circle . A and B are point P outside the circle . A and B are point on the circle . If ∠PAB=47∘ , then ∠OAB is equal to :
View Solution
