एक अर्द्धगोलाकार बिन्दु, किसी एकसमान विद्युत क्षेत्र में रखा है इसके वक्र पृष्ठ से सम्बद्ध फ्लक्स क्या है यदि विद्युत क्षेत्र है (अ) इसके आधार पर समांतर (चित्र अ) तथा (ब) इसके आधार के लम्बवत (चित्र ब)।
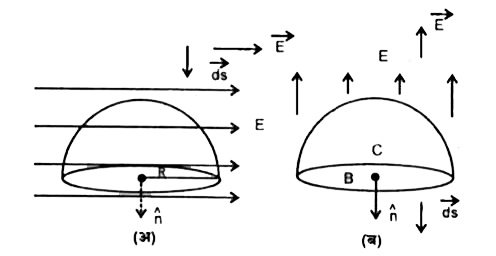
अर्द्धवृत्ताकार पिण्ड को एक बन्द वस्तु की तरह मानते है जो एक वक्र पृष्ठ तथा एक समतल आधार से निर्मित है तो पिण्ड से सम्बद्ध कुल विद्युत फ्लक्स शून्य होगा क्योकि पिण्ड में कोई आवेश परिबद्ध नहीं है। अतः यदि ϕc व ϕb क्रमशः वक्र पृष्ठ तथा आधार की सम्बद्ध फ्लक्स है तो
ϕ=ϕC+ϕS=0
या ϕC=−ϕB
चित्र (अ) की परिस्थिति में आधार का सदिश क्षेत्रफल, →E के लम्बवत है अतः ϕB=0 तथा इस कारण ϕC=0
चित्र (ब) की परिस्थिति में आधार का सदिश क्षेत्र →E के प्रति समान्तर है अतः ϕB=Ecos180∘=−EπR2
अतः ϕC=−ϕB=EπR2
(यहाँ यह स्पष्ट है कि वक्र पृष्ठ से सम्बन्ध फ्लक्स काट क्षेत्र की त्रिज्या पर निर्भर है पर वक्र पृष्ठ की आकृति पर नहीं)
Topper's Solved these Questions
- गाउस का नियम एवं उसके अनुप्रयोग BOOK - MITTAL PUBLICATIONCHAPTER - गाउस का नियम एवं उसके अनुप्रयोग EXERCISE - आंकिक उदाहरण (विद्युत फ्लक्स पर आधारित)
6 Videos
- गाउस का नियम एवं उसके अनुप्रयोग BOOK - MITTAL PUBLICATIONCHAPTER - गाउस का नियम एवं उसके अनुप्रयोग EXERCISE - पाठ्य पुस्तक के प्रश्न एवं उनके उतर - बहुचयनात्मक प्रश्न
10 Videos
- गाउस का नियम एवं उसके अनुप्रयोग BOOK - MITTAL PUBLICATIONCHAPTER - गाउस का नियम एवं उसके अनुप्रयोग EXERCISE - गाउस नियम पर आधारित (उदाहरण)
31 Videos
- किरण प्रकाशिकी BOOK - MITTAL PUBLICATIONCHAPTER - किरण प्रकाशिकी EXERCISE - प्रतियोगी परीक्षा संबंधित प्रश्न
20 Videos
- चुम्बकत्व एवं चुम्बकीय पदार्थो के गुणBOOK - MITTAL PUBLICATIONCHAPTER - चुम्बकत्व एवं चुम्बकीय पदार्थो के गुणEXERCISE - प्रतियोगी परीक्षा संबंधी प्रश्न (बहुविकल्पीय प्रश्न)
18 Videos
Similar Questions
10 मी2 क्षेत्रफल के आयताकार फ्रेम को 20 वोल्ट/मीटर के विद्युत क्षेत्र में इस प्रकार रखा गया है कि फ्रेम का तल विद्युत क्षेत्र की दिशा से 30∘ का कोण बनाता है। फ्रेम से गुजरने वाला विद्युत फ्लक्स क्या है?
View Solutionएक समरूप आवेशित ठोस अचालक गोले के कारण विद्युत क्षेत्र की तीव्रता अधिकतम होती है-
View Solution+4μC,+6μC,+3μC एवं −9μC के चार आवेश किसी बन्द पृष्ठ के भीतर स्थित है तथा का आवेश पृष्ठ के बाहर है। पृष्ठ से निर्गत कुल विद्युत फ्लक्स ज्ञात कीजिए।
(ε0=8.86×10−12C2N−1m−2)
View Solutionएक कार में पश्च दृश्य दर्पण के रूप में 20 सेमी फोकस दूरी का उत्तल दर्पण प्रयुक्त किया जाता है। एक दूसरी कार जो इस कार से 2.8 m की दूरी पर पीछे है, यदि पहली कार का सापेक्ष वेग 15 मी./से है, तो दूसरी कार के प्रतिबिम्ब की, प्रथम कार के पश्च दृश्य दर्पण में चाल है -
View Solutionएक छड़ चुम्बक को कॉटन के पतले धागे से एक समान चुम्बकीय क्षेत्र में लटकाया गया है और यह साम्य में है। इसे 60∘ घुमाने के लिए आवश्यक ऊर्जा W है। इस नई परिस्थिति में रखने के लिए आवश्यक बल आघूर्ण होगा -
View Solutionएकसमान विद्युत क्षेत्र E=3×103ˆi(N)/C पर विचार कीजिये ।
(a) इस क्षेत्र का 10 cm भुजा के वर्ग के उस पार्श्व से जिसका तल yz तल के समांतर है, गुजरने वाला फ्लक्स क्या है ?
(b) इस वर्ग से गुजरने वाला फ्लक्स कितना है यदि इसके तल का अभिलंब x- अक्ष से 60∘ कोण बनता है ?
View Solutionएकसमान विद्युत क्षेत्र E=3×103ˆi(N)/C पर विचार कीजिये।
(a) इस क्षेत्र का 10 cm भुजा के वर्ग के उस पार्श्व से जिसका तल yz तल के समांतर है, गुजरने वाला फ्लक्स क्या है ?
(b) इस वर्ग से गुजरने वाला फ्लक्स कितना है यदि इसके तल का अभिलंब x- अक्ष से 60∘ कोण बनता है ?
एकसमान विद्युत क्षेत्र का 20 cm भुजा के किसी घन से (जो इस प्रकार अभिविन्यासित है की उसके फलक निर्देशांक तलों के समांतर है ) कितना नेट फ्लक्स गुजरेगा ?
View Solutionनिम्नलिखित में से किसी एक शब्द का भाववाचक संज्ञा रूप लिखिए :
(अ) सच्चा। (ब) चंचल।
View Solutionनिम्नलिखित में से किसी एक शब्द का विशेषण रूप लिखिए :
(अ) रसायन | (ब) पुराण|
View Solutionमुख की है शोभा प्रिय वचनों से, …………………. से नहीं। ( अ ) चंदन ( ब ) चांदी ( क ) सुगंध
View Solutionदिये गये चित्र में छायांकित भाग निम्न सुसंगत क्षेत्र को दर्शाता है -
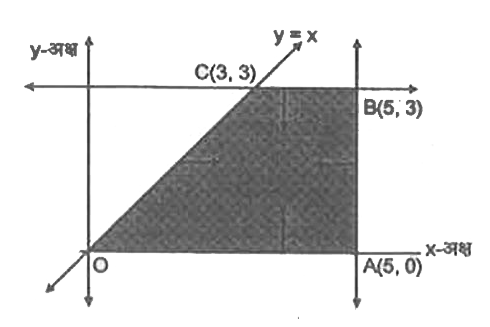
तो प्रतिबन्ध है -
View Solutionचित्र में दिखाए गए छायांकित क्षेत्र के लिए असामिका है-
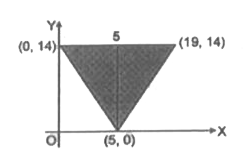
View Solutionयदि एक वक्र बिंदु (1, -2) से होकर जाता है तथा इस पर किसी बिंदु (x, y) पर स्पर्श रेखा का ढाल (slope) x2−2yx है, तो यह वक्र निम्न में से किस बिंदु से होकर जाता है ?
View Solutionएक द्विध्रुव 10 सेमी लम्बा तथा आवेश 500μC से बना है। इसके अक्ष से 25 सेमी दूरी पर विद्युत क्षेत्र की तीव्रता होगी
View Solutionअब कहाँ दूसरे के दुःख से दुःखी होने वाले' पाठ के आधार पर लिखिए कि प्रकृति में असंतुलन क्यों हो रहा है? इसके परिणाम क्या हैं ?
View Solutionकैसी मधुर' मनोहर उज्ज्वल है यह प्रेम-कहानी। जी में है अक्षर बन इसके ब। विश्व की रानी। प्रस्तुत पद्यांश किस पाठ से संकलित है?
View Solution
