एक R त्रिज्या की पतली वल्य पर q आवेश एक समान रूप से वितरित है। वलय की अक्ष पर, केन्द्र से x दूरी पर स्थित बिन्दु पर विधुत क्षेत्र की तीव्रता ज्ञात कीजिए। प्राप्त परिणाम की प्रतिबन्ध $x > > R$ के लिए विवेचना कीजिए।

Video Solution

Text Solution

Verified by Experts

चूँकि वल्य पर q आवेश एक समान रूप से वितरित है अतः रेखीय आवेश घनत्व

$λ = \frac{q}{L} = \frac{q}{2 π R}$
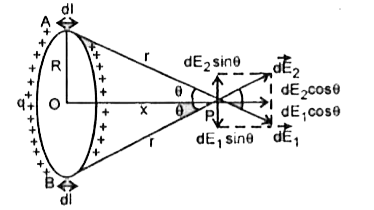
अब चित्र में दर्शाइए अनुसार हम वलय पर व्यासतः सम्मुख दो समान लम्बाई dl के अल्पांश A एवं B लेते है।
प्रत्येक अल्पांश पर आवेश
$d q = λ d l$
प्रत्येक अल्पांश से बिन्दु P की दूरी r है, तो
अल्पांश A के कारण बिन्दु P पर विद्युत क्षेत्र
$d E_{1} = \frac{1}{4 π \in_{0}} \frac{d q}{r^{2}}$ {AP दिशा में}
अल्पांश B के कारण बिन्दु P पर विद्युत क्षेत्र
$d E_{2} = \frac{1}{4 π \in_{0}} \frac{d q}{r^{2}}$ {BP दिशा में}
स्पष्टतः $| d E_{1} | = | d E_{2} |$
$d E_{1}$ एवं $d E_{2}$ को चित्रानुसार वियोजित करने पर इनके ऊर्ध्वघटक $d E_{1} sin θ$ एवं $d E_{2} sin θ$ परिमाण में समान एवं परस्पर विपरीत होने के कारण परस्पर निरस्त हो जाते है जबकि क्षैतिज घटक $d E_{1} cos θ$ एवं $d E_{2} cos θ$ समान दिशा में होने के कारण जुड़ जाते है। हम सम्पूर्ण वलय को इसी प्रकार के अल्पांश युग्मो में विभक्त कर सकते है। प्रत्येक युग्म का क्षैतिज घटक OP दिशा के अनुदिश होता है अतः सम्पूर्ण वलय के कारण बिन्दु P पर विद्युत क्षेत्र
$E = \int_{L} d E cos θ = \frac{1}{4 π \in_{0}} \int_{L} \frac{d q}{r^{2}} cos θ$
$∵$ चित्र से $cos θ = \frac{x}{r}, ∵ d q = λ d l$ तथा $x, λ$ एवं r नियतांक है।
अतः $E = \frac{λ x}{4 π \in_{0} r^{3}} \int_{L} d l$
$∵ \int_{L} d l$ = सम्पूर्ण वलय की लम्बाई $= 2 π R$
अतः $E = \frac{λ x}{4 π \in_{0} r^{3}} 2 π R$
$∵ λ \times 2 π R = q$ तथा चित्र से $r = {(R^{2} + x^{2})}^{1 / 2}$
अतः $E = \frac{q x}{4 π \in_{0} {(R^{2} + x^{2})}^{3 / 2}} = \frac{k q x}{{(R^{2} + x^{2})}^{3 / 2}}$
प्रतिबन्ध $x > > R$ के लिए उपरोक्त सूत्र
$E = \frac{k q x}{x^{3}} = \frac{k q}{x^{2}}$
में लघुकृत हो जाता है। यह सूत्र किसी बिन्दु आवेश q से x दूरी पर स्थित बिन्दु पर विद्युत क्षेत्र के सूत्र के समान ही है। अतः अक्ष पर दूरस्थ बिन्दुओं के लिए वलय इस प्रकार व्यवहार करती है मानो इसका सम्पूर्ण आवेश इसके केन्द्र पर संकेन्द्रित है।

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROSTATICS

Topper's Solved these Questions

Similar Questions

MITTAL PUBLICATION-गाउस का नियम एवं उसके अनुप्रयोग -पाठ्य निहित उदाहरण

Home
Ask Doubt
Profile