Show that area of the parallelogram whose diagonals are given by $\vec{a} and \vec{b}$ is $\frac{| \vec{a} \times \vec{b} |}{2}$ Also, find the area of the parallelogram whose diagonals are $2 i - j + k and i + 3 j - k .$

Video Solution

Text Solution

Verified by Experts

Let ABCD be a parallelogram such that

$\vec{A B} = \vec{p}, \vec{A D} = \vec{q} \Rightarrow \vec{B C} = \vec{q}$
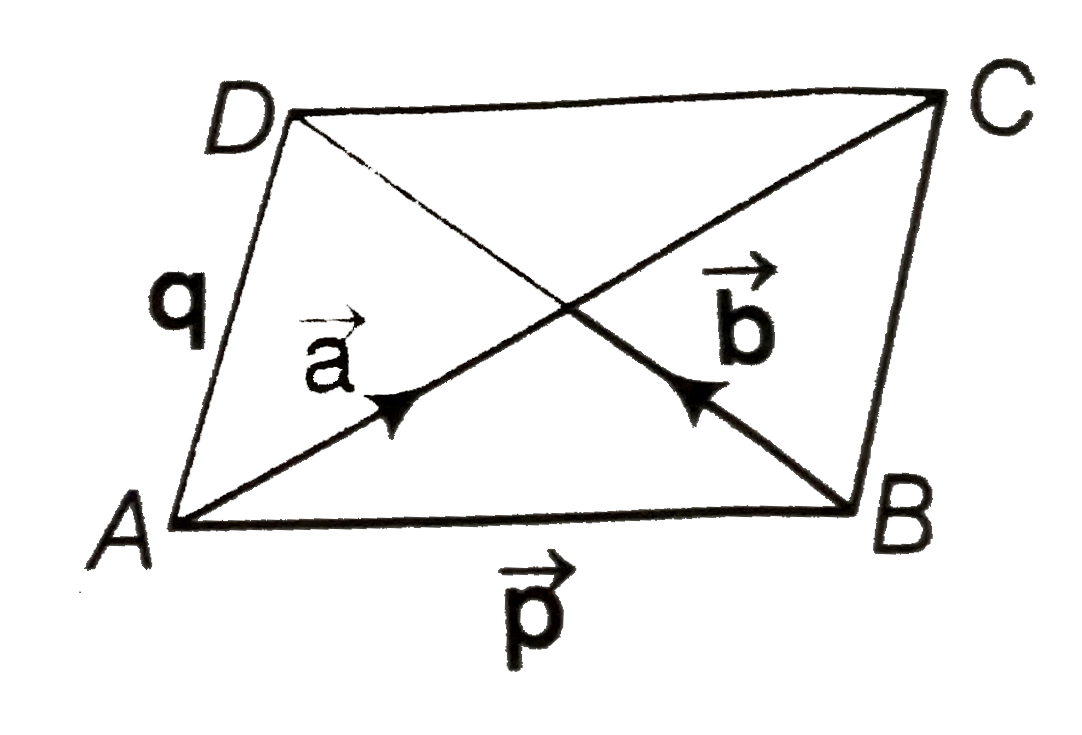
By triangle law of addition, we get
$\vec{A C} = \vec{p} + \vec{p} = \vec{a} [s a y ... ... (i)]$
Similarly. $\vec{B D} = - \vec{p} + \vec{p} = \vec{b} [s a y ... ... (i i)]$
By adding Eqs. (i) and (ii), we get
$\vec{a} + \vec{b} = 2 \vec{q} \Rightarrow \vec{q} = \frac{1}{2} (\vec{a} + \vec{b})$
On subtracing Eq.(ii) from (i) we get
$\vec{a} - \vec{b} = 2 \vec{b} \Rightarrow \vec{p} = \frac{1}{2} (\vec{a} + \vec{b})$
Now , $\vec{p} \times \vec{q} = \frac{1}{4} (\vec{a} - \vec{b}) \times (\vec{a} - \vec{b})$
$= \frac{1}{4} (\vec{a} \times \vec{a} + \vec{a} \times \vec{b} - \vec{b} \times \vec{a} - \vec{b} \times \vec{b})$
$= \frac{1}{4} [\vec{a} \times \vec{b} + \vec{a} \times \vec{b}]$
$= \frac{1}{2} (\vec{a} \times \vec{b})$
So, aera fo a parallelogram $A B C D = | \vec{p} \times \vec{q} | = \frac{1}{2} | \vec{a} \times \vec{b} |$
Now, area of a parallelogram, whhose diagonals are $2 \hat{i} - \hat{j} + \hat{k} and \hat{i} + 3 \hat{j} - \hat{k}$ .
$= \frac{1}{2} | (2 \hat{i} - \hat{j} + \hat{k}) \times (\hat{i} + 3 \hat{j} - \hat{k}) |$
$= \frac{1}{2} | \begin{matrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & - 1 & 1 \\ 1 & 3 & - 1 \end{matrix} |$
$= \frac{1}{2} | [\hat{i} (1 - 3) - \hat{j} (- 2 - 1) + \hat{k} (6 + 1)] |$
$= \frac{1}{2} | - 2 \hat{i} + 3 \hat{j} + 7 \hat{k} |$
$= \frac{1}{2} \sqrt{4 + 9 + 49}$
$\frac{1}{2} \sqrt{62}$ sq units

|

Updated on:21/07/2023

Class 12 MATHS VECTOR ALGEBRA

Topper's Solved these Questions

BOOK - NCERT EXEMPLARCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - Three Dimensional Geometry
46videos
THREE DIMENSIONAL GEOMETRY

Similar Questions

Knowledge Check

Question 1 - Select One
The area of a parallelogram having diagonals $a = 3 i + j - 2 k and b = i - 3 j + 4 k$ is
A $5 \sqrt{3}$
B $2 \sqrt{3}$
C $4 \sqrt{3}$
Dnone of these

NCERT EXEMPLAR-VECTOR ALGEBRA-Vector Algebra

Home
Ask Doubt
Profile