Prove that the area of the parallelogram with diagonal →a and →b is 12∣∣→a×→b∣∣
Let ABCD is a parallelogram with A as the origin. Let the position vector of B and D be →p and →q respectively. Then
−−→AB=→p and −−→AD=→q
But −−→BC=−−→AD Therefore −−→BC=→q
By triangle law of addition
−−→AB+−−→BC=−−→AC
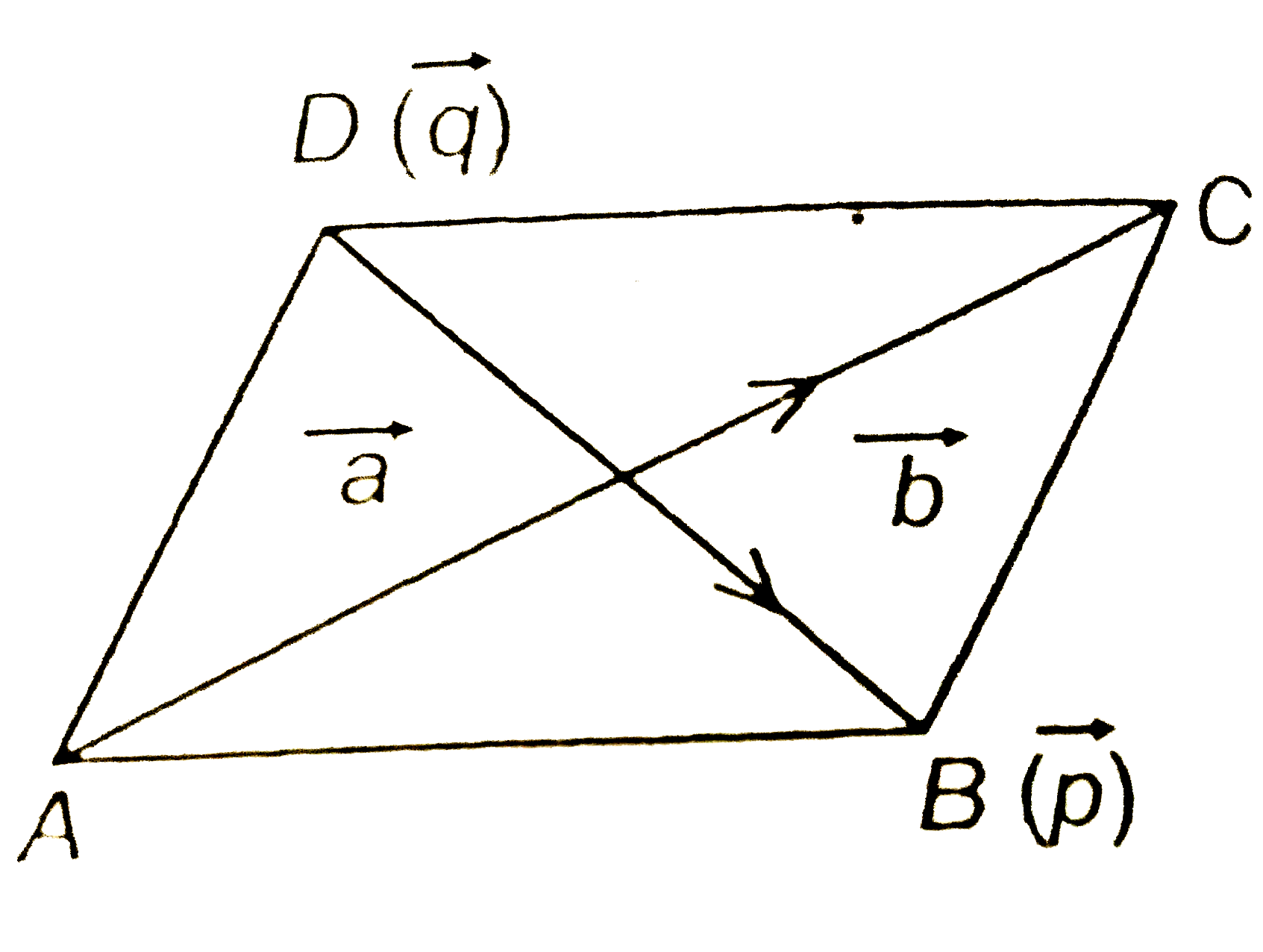
→p+→q=−−→AC
→p+→q=→a .......(i)
−−→BD=postion vector of D-positon vector of B.
⇒ →b=→q−→p .......(ii)
Adding (i) and (ii), we get
2→q=→a+→b⇒→q=12(→a+→b)
Subtracting (ii) from (i), we get
2→p=→a−→b⇒→p=12(→a−→b)
Now →p×→q=12(→a−→b)×12(→a+→b)
⇒→p×→q=14[(→a−→b)×(→a+→b)]
⇒→p×→q=14[→a×→a+→a×→b−→b×→a−→b×→b]
⇒ →p×→q=14[→a×→b+→a×→b]
⇒ →p×→q=12(→a×→b)
So, the area of parallelogram ABCD =|→p×→q|=12∣∣→a×→b∣∣
Topper's Solved these Questions
- VECTOR ALGEBRABOOK - AAKASH INSTITUTECHAPTER - VECTOR ALGEBRAEXERCISE - ILLUSTRATION
1 Videos
- VECTOR ALGEBRABOOK - AAKASH INSTITUTECHAPTER - VECTOR ALGEBRAEXERCISE - TRY YOURSELF
20 Videos
- TRIGNOMETRIC FUNCTIONS BOOK - AAKASH INSTITUTECHAPTER - TRIGNOMETRIC FUNCTIONS EXERCISE - Section - J (Akash Challengers Question)
15 Videos
Similar Questions
Show that area of the parallelogram whose diagonals are given by →a and →b is ∣∣→a×→b∣∣2. Also, find the area of the parallelogram, whose diagonals are 2ˆi−ˆj+ˆk and ˆi+3ˆj−ˆk.
View SolutionIf the area of the parallelogram with →a and →b as two adjacent sides is 15 sq unit ,than the area of the parallelogram having, 3→a+2→b and →a+3→b as two adjacent sides in sq unit is
View Solution
Knowledge Check
Let →a,→b and →c be three non zero vectors.
The area of the parallelogram formed by →a and →b as diagonals is →a=ˆi−2ˆj
→b=2ˆi+ˆj+3ˆkA70B35C√70/2D√70The length of the longer diagonal of the parallelogram constructed on 5→a+2→band→a−3→b, if it is given that |→a|=2√2,∣∣→b∣∣=3and→a.Vecb=π4 is
A15B√3C√593D√369
find the area of a parallelogram whose diagonals are →a=3ˆi+ˆj−2ˆkand→b=ˆi−3ˆj+4ˆk.
View SolutionShow that the components of →b parallel to →a and perpendicular to it are (→a.→b)→a→a2and((→a×→b)→a))a2 respectively.
View SolutionShow that (→a+→b)×(→a−→b)=−2(→a×→b) and use this result to find the area of a parallelogram whose diagonals are
ˆi−2ˆj−3ˆkand2ˆi−3ˆj+2ˆk
View SolutionIf the non zero vectors →aand→b are perpendicular to each other then the solution the equation →r×→a=→b is (A) →rα→b−1∣∣→b∣∣2(→a×→b) (B) →rα→b+1|→a|2(→a×→b) (C) →rα→b+1∣∣→b∣∣2(→a×→b) (D) none of these
View SolutionIf →aand→b are two such that |→a|=5,∣∣→b∣∣=4and∣∣→a.→b∣∣=10, find the angel between →aand→b and hence find ∣∣→a×→b∣∣
View SolutionIf →a→b be any two mutually perpendiculr vectors and →α be any vector then ∣∣→a×→b∣∣2(→a.→α)→a→a∣2+∣∣→ax→b∣∣2(→b.→α)→b∣∣→b∣∣2−∣∣→a×→b∣∣2→α= (A) ∣∣(→a.→b)→α∣∣(→a×→b) (B) [→a→b→α](→b×→a) (C) [→a→b→α](→a×→b) (D) none of these
View Solution
