The vector →a+→b bisects the angle between the non-collinear vectors →aand→b, if……..
If vector →a+→b bisects the angle between the non-collinear vectors, then
→a.(→a+→b)=|→a|.∣∣→a+→b∣∣cosθ
→a.(→a+→b)=a√a2+b2cosθ
⇒cosθ=→a.(→a+→b)a√a2+b2......(i)
→b.(→a+→b)=∣∣→b∣∣.∣∣→a+→b∣∣cosθ
and →b.(→a+→b)=b√a2+b2cosθ [since, θ should be same]
⇒cosθ=→b.(→a+→b)b√a2+b2........(ii)
From Eqs. (i) and (ii),
→a.(→a+→b)a√a2+b2=→b.(→a+→b)b√a2+b2⇒→a|→a|=→b∣∣→b∣∣
∴ˆa=ˆb⇒ˆaandˆb are equal vectors.
Topper's Solved these Questions
Similar Questions
Knowledge Check
If →aand→b are two vectors, such that →a.→b<0and∣∣→a.→b∣∣=∣∣→a×→b∣∣ then the angle between angles between the vectors →aand→b is
AπB7π/4Cπ/4D3π/4If the angle between two vectors →Aand→B is 90∘ then
A→A=2→BB→A−→B=→0C∣∣→A+→B∣∣=∣∣→A−→B∣∣D→A+→B=→0if →a and →b non-zero ad non-collinear vectors, then
A→a×→b=[→a→bˆi]ˆi+[→a→bˆj]ˆj+[→a→bˆk]ˆkBveca.vecb=(veca.hati)(vecb.hati)+(veca.hatj)(vecb.hatj)+(veca.hatk)(vecb.hatk)Cif →u=ˆa−(ˆa.ˆb)ˆb and →v=ˆa׈b then |→v|=|→u|Dif →c=→a×(→a×→b), then →c.→a=0
Given : →P=→A+→Band→Q=→A−→B. If the magnitudes of vectors →Pand→Q are equal, what is the angle between vectors →Aand→B?
View SolutionConsider three vectors →a,→band→c. Vectors →aand→b are unit vectors having an angle θ between them For vector veca,|→a|2=→a.→a If →a⊥→band→a⊥→cthen→a∣∣→b×→c If →a∣∣→b,then→a=t→b Now answer the following question: If →c is a unit vector and equal to the sum of →aand→b the magnitude of difference between →aand→b is (A) 1 (B) √2 (C) √3 (D) 1√2
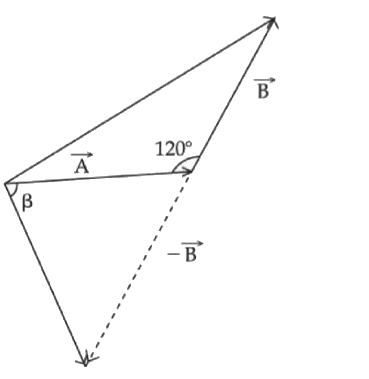
View SolutionThe angle between vector (→A) and (→A−→B) is :
View SolutionIf →a,→b,→c are vectors such that →a+→b+→c=0and|→a|=7,∣∣→b∣∣=5,|→c|=3 then angle between vector →band→c is
View SolutionLet →a,→b and →c be non-zero vectors such that no two are collinear and
(→a×→b)×→c=13∣∣→b∣∣|→c|→a
If θ is the acute angle between the vectors →b and →c then sinθ equals
View Solution

