The angle between vector (→A) and (→A−→B) is :
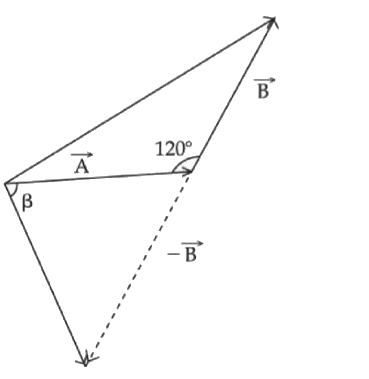
A
tan−1⎛⎜⎝−B2A−B√32⎞⎟⎠
B
tan−1(√3B2A−B)
C
tan−1(A0.7B)
D
tan−1(BcosθA−Bsinθ)
Video Solution
Text Solution
The correct Answer is:B
|
Answer
Step by step video & image solution for The angle between vector (vecA) and (vecA-vecB) is : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- JEE MAINS 2021Book:JEE MAINS PREVIOUS YEARChapter:JEE MAINS 2021Exercise:Physics (Section B )
Explore 10 Videos
- JEE MAINS 2021Book:JEE MAINS PREVIOUS YEARChapter:JEE MAINS 2021Exercise:Physics (Section B)
Explore 40 Videos
- JEE MAINS 2020Book:JEE MAINS PREVIOUS YEARChapter:JEE MAINS 2020Exercise:PHYSICS
Explore 246 Videos
- JEE MAINS 2022Book:JEE MAINS PREVIOUS YEARChapter:JEE MAINS 2022Exercise:PHYSICS (SECTION -B)
Explore 10 Videos
Similar Questions
Knowledge Check
The angle between vectors (→A×→B)and(→B×→A) is :
Aπ radBπ2 radCπ4 radDzeroIf the angle between the vectors →Aand→B is θ, the value of the product (→B×→A)⋅→A is equal to
ABA2cosθBBA2sinθCBA2sinθcosθDZeroIf the angle between the vectors →Aand→B is θ, the value of the product (→B×→A)⋅→A is equal to
ABA2cosθBBA2sinθCBA2sinθcosθDzero
What will be the angle between the vectors →Aand→B if →A+→B=→R and A2+B2=R2?
View SolutionIf the angle between unit vectors →aand→bis60∘ . Then find the value of ∣∣→a−→b∣∣.
View SolutionIf the angle between two vectors →Aand→B is 90∘ then
View SolutionIf →A+→B=→C and |A|2+|B|2=|C|2 , then angle between vectors →A and →B would be
View SolutionThe vector →A and →B are such that ∣∣→A+→B∣∣=∣∣→A−→B∣∣. The angle between vectors →A and →B is -
View Solution

