Find the equations the sides of an isosceles right angled triangle the equation of whose hypotenuse is 3x+4y=4 and the opposite vertex is the point (2, 2).
The correct Answer is:N/a
Let slope of line AC be m and slope of line BC is −34 and let angle between line AC and BC be θ
∴tanθ=∣∣
∣∣m+341−3m4∣∣
∣∣⇒tan45∘=±⎡⎣m+341−3m4⎤⎦
Taking positive sign, 1=m+341−3m4
⇒m+34=1−3m4
⇒m+3m4=1−34
⇒7m4=14⇒m=17
Taking negative sign, 1=m+341−3m4
⇒m+34=1−3m4
⇒m+3m4=1−34
⇒7m4=14⇒m=17
Taking negative sign,
1=⎛⎝m+341−3m4⎞⎠⇒1−3m4=−m−34
⇒m−3m4=−1−34
⇒3m4=−74⇒m=−7
∴ Equation of side AC having slope (17) is
y−2=17(x−2)
⇒7y−14=x−2
⇒x−7y+12=0
and equation of side AB having slope (−7) is
y−2=−7(x−2)
⇒y−2=−7x+14
⇒7x+y−16=0
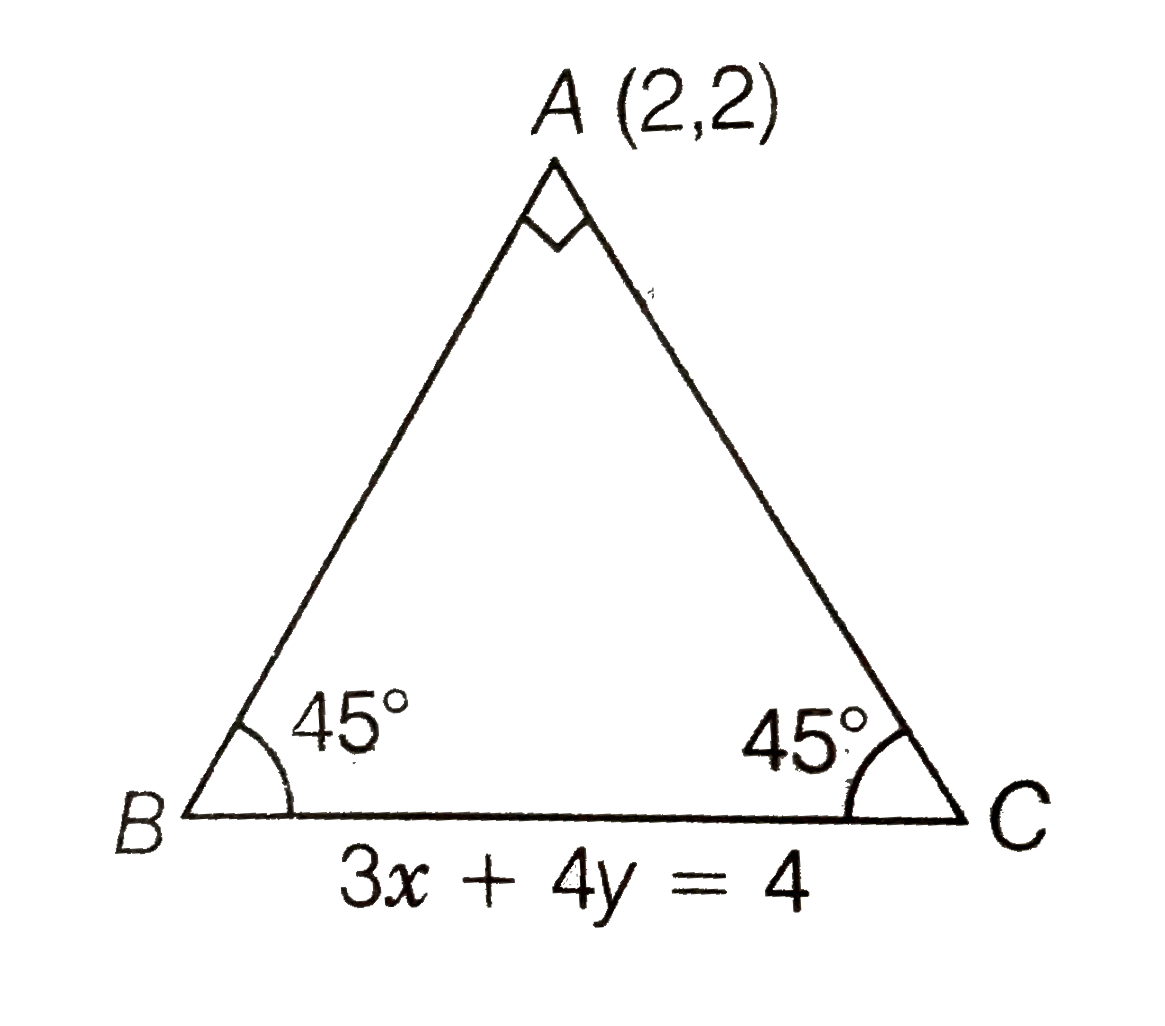
Topper's Solved these Questions
- STRAIGHT LINESBOOK - NCERT EXEMPLARCHAPTER - STRAIGHT LINESEXERCISE - Long Answer type
9 Videos
- STRAIGHT LINESBOOK - NCERT EXEMPLARCHAPTER - STRAIGHT LINESEXERCISE - Objective type questions
20 Videos
- STATISTICSBOOK - NCERT EXEMPLARCHAPTER - STATISTICSEXERCISE - FILLERS
7 Videos
- TRIGONOMETRIC FUNCTIONS BOOK - NCERT EXEMPLARCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - TRUE/FALSE
9 Videos
Similar Questions
Find the equations to the sides of an isosceles right angled triangle the equation of whose hypotenuse is 3x+4y=4 and the opposite vertex is the point (2,2).
View SolutionA side of an isosceles right angled triangle is x. Find its hypotenuse.
View SolutionA side of an isosceles right angled triangle is x. Find its hypotensuse.
View SolutionThe area of an isosceles right - angled triangle is 72 cm2 .Find its hypotenuse .
View SolutionFind the equation of the legs of a right isosceles triangle if the equation of its hypotenuse is x−2y−3=0 and the vertex of the right angle is at the point (1,6),
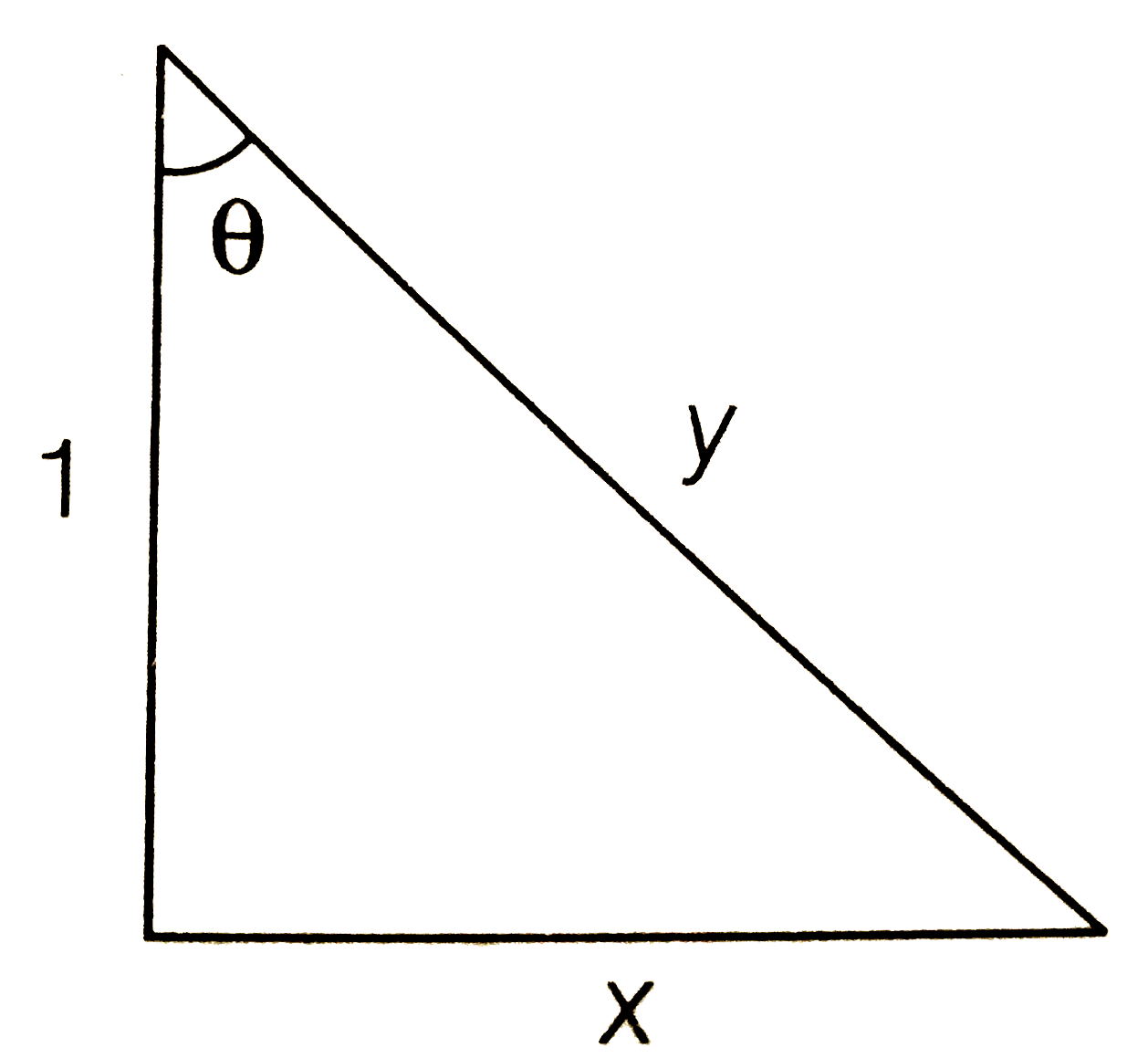
View SolutionA right angled triangle has legs 1 and x. The hypotenuse is y and angle opposite to the side x is θ. Shown as

View SolutionFind the area of an isosceles right triangle whose hypotenuse is 4√2 cm
View SolutionThe area of an isosceles right triangle is 200 m^2. Find its hypotenuse.
View SolutionThe equation of the circumcircle of the triangle, the equation of whose sides are y=x,y=2x,y=3x+2, is
View SolutionFind the equations of the medians of a triangle, the equations of whose sides are: 3x+2y+6=0, 2x−5y+4=0 and x−3y−6=0
View Solution
