If the intercept of a line between the coordinate axes is divided by the point (−5,4) in the ratio 1:2, then find the equation of the line.

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:N/a

Let intercept of a line are (h,k).
The coordinates of A and B are (h,0)and (0.k)respectively.
−5=1×0+2×h1+2
⇒−5=2h3⇒+h=−152
and 4=1.k+0.21+2
⇒K=12
∴A=(−152,0) and B=(0,12)
Hence the equation of a line AB is
y−0=12−00+15/2(x+152)
⇒y=12.215(x+152)
⇒5y=8x+60⇒8x−5y+60=0
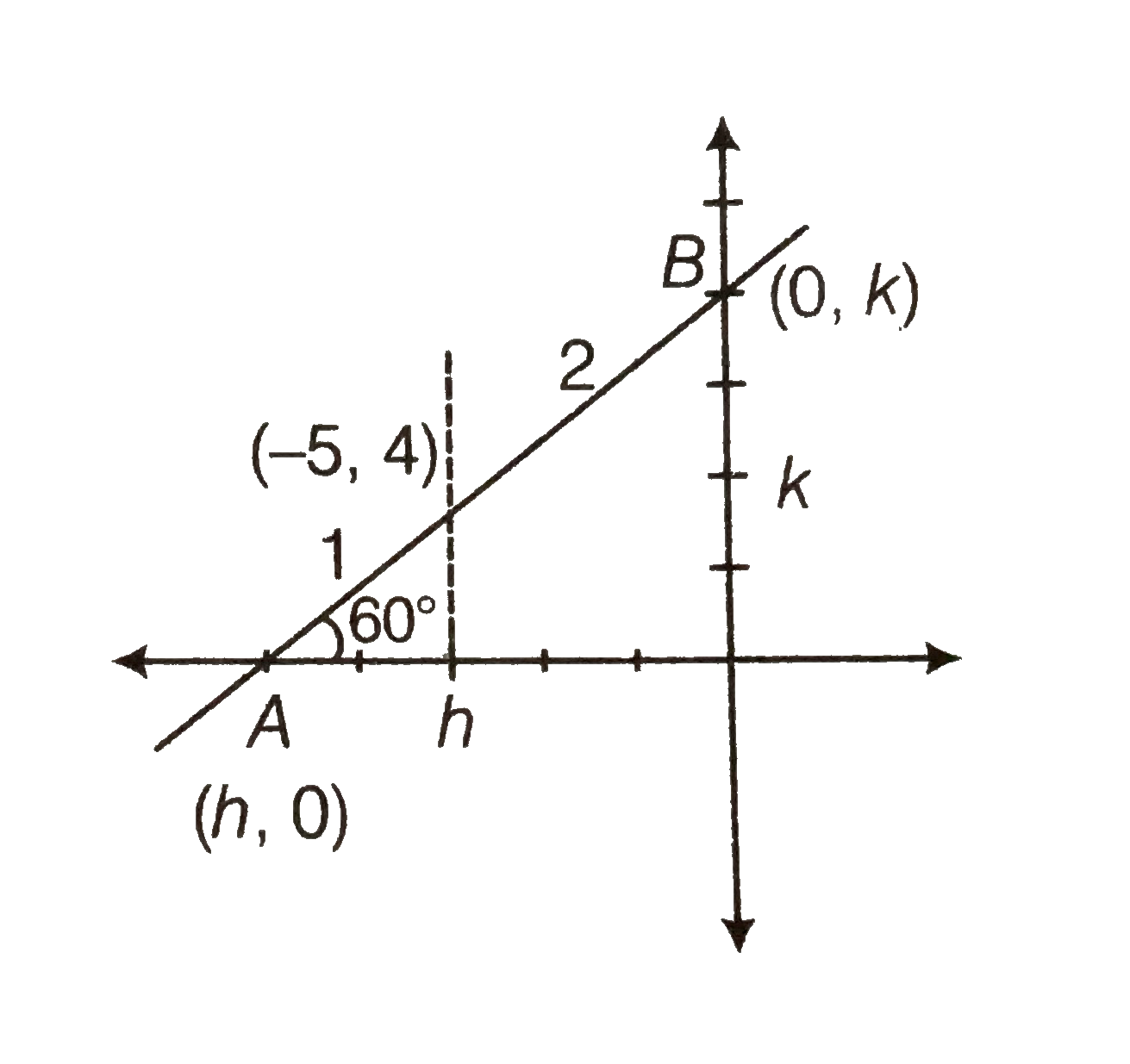
ocr_image

Updated on:21/07/2023
|
Class 11MATHSSTRAIGHT LINES

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • If the portion of a line intercepted between the coordinate axes is divided by the point (2,−10 in the ratio 3:2. then the equation of that line is

    A5x−2y−20=0
    B2x−y−5=0
    C3x−y−7=0
    Dx−3y−5=9

  • An equation of a line whose segment between the coordinate axis is divided by the point (12,13) in the ratio 2:3 is

    A6x+9y=5
    B9x+6y=5
    C4x+9y=5
    D9x+4y=5