A stationary object is released from a point P a distance 3R from the centre of the moon which has radius R and mass M. which one of the following expressions gives the speed of the object on hitting the moon?

A

${(\frac{2 G M}{3 R})}^{\frac{1}{2}}$

B

${(\frac{4 G M}{3 R})}^{\frac{1}{2}}$

C

${(\frac{2 G M}{R})}^{\frac{1}{2}}$

D

${(\frac{G M}{R})}^{\frac{1}{2}}$

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:B

To solve the problem of finding the speed of an object when it hits the surface of the moon after being released from a distance of $3 R$ from the center of the moon, we can use the principle of conservation of energy. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the System
We have:
- A stationary object of mass $m$ released from a point $P$ at a distance $3 R$ from the center of the moon.
- The moon has a radius $R$ and mass $M$ .
Step 2: Identify Potential Energy
The gravitational potential energy $U$ at a distance $r$ from the center of a mass $M$ is given by the formula:
$U = - \frac{G M m}{r}$
where $G$ is the gravitational constant.
Step 3: Calculate Initial Potential Energy
At point $P$ (distance $3 R$ from the center of the moon):
$U_{P} = - \frac{G M m}{3 R}$
Step 4: Calculate Final Potential Energy
When the object hits the surface of the moon (distance $R$ from the center):
$U_{Q} = - \frac{G M m}{R}$
Step 5: Use Conservation of Energy
According to the conservation of energy, the change in potential energy will equal the kinetic energy gained by the object. Therefore:
$Δ U = K$
where $K$ is the kinetic energy given by:
$K = \frac{1}{2} m v^{2}$
Step 6: Calculate Change in Potential Energy
The change in potential energy as the object moves from point $P$ to point $Q$ is:
$Δ U = U_{Q} - U_{P} = (- \frac{G M m}{R}) - (- \frac{G M m}{3 R})$
$Δ U = - \frac{G M m}{R} + \frac{G M m}{3 R}$
$Δ U = - \frac{3 G M m}{3 R} + \frac{G M m}{3 R} = - \frac{2 G M m}{3 R}$
Step 7: Set Change in Potential Energy Equal to Kinetic Energy
Now we set this equal to the kinetic energy:
$- \frac{2 G M m}{3 R} = \frac{1}{2} m v^{2}$
Step 8: Solve for $v^{2}$
We can cancel $m$ from both sides (assuming $m \neq 0$ ):
$- \frac{2 G M}{3 R} = \frac{1}{2} v^{2}$
Multiplying both sides by 2:
$- \frac{4 G M}{3 R} = v^{2}$
Step 9: Take the Square Root
Taking the square root to find $v$ :
$v = \sqrt{\frac{4 G M}{3 R}}$
Final Expression
Thus, the speed of the object when it hits the moon is:
$v = \sqrt{\frac{4 G M}{3 R}}$

Updated on:18/9/2024

|

Class 12 PHYSICS NTA JEE MOCK TEST 42

Topper's Solved these Questions

Similar Questions

Knowledge Check

A point mass $m$ is released from rest at a distance of $3 R$ from the centre of a thin-walled hollow sphere of radius $R$ and mass $M$ as shown. The hollow sphere is fixed in position and the only force on the point mass is the gravitational attraction of the hollow sphere. There is a very small hole in the hollow sphere through which the point mass falls as shown. The velocity of a point mass when it passes through point $P$ at a distance $R / 2$ from the centre of the sphere is

A $\sqrt{\frac{2 G M}{3 R}}$
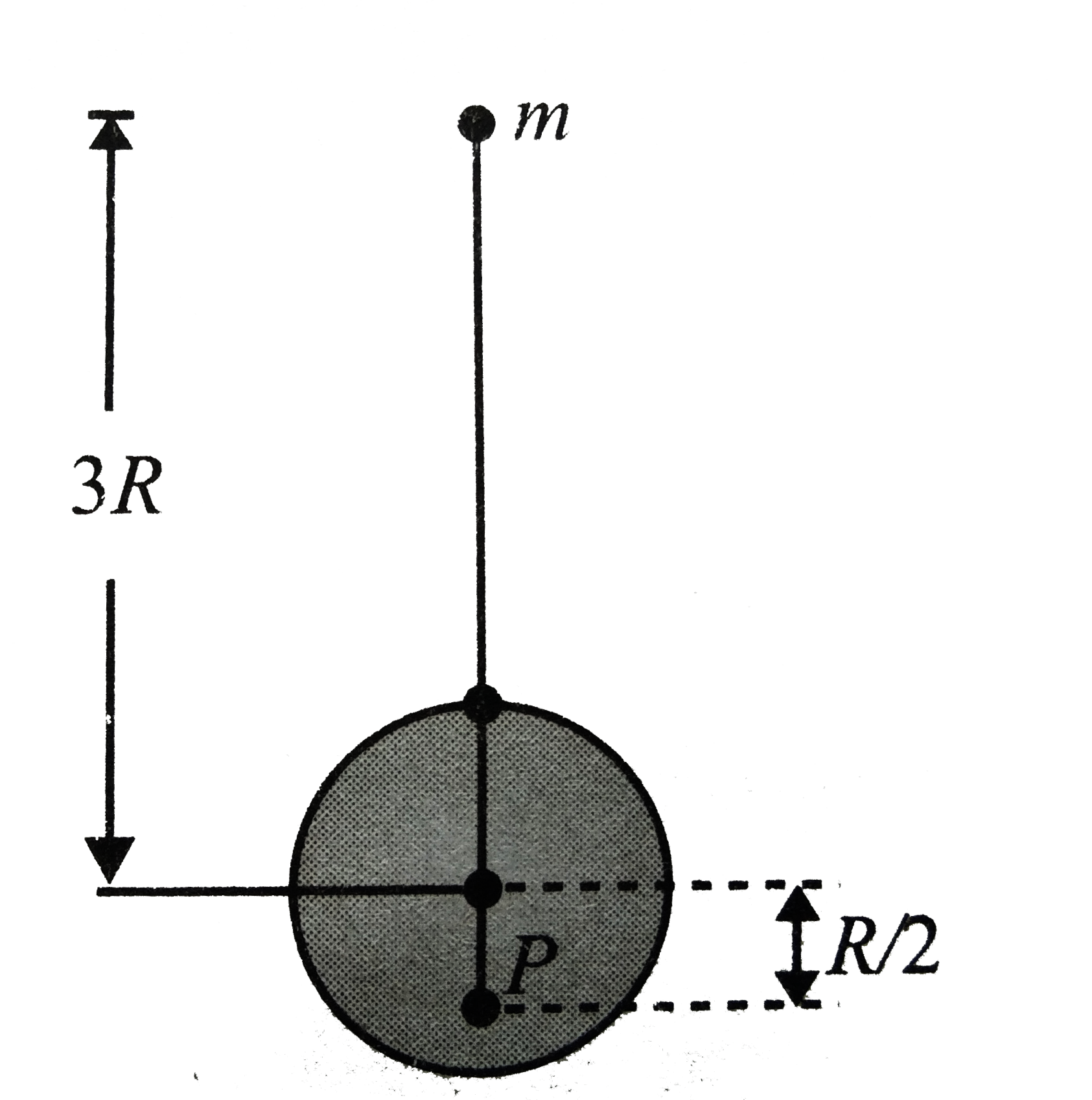B $\sqrt{\frac{5 G M}{3 R}}$
C $\sqrt{\frac{25 G M}{24 R}}$
Dnone of these
A block of mass m is released from rest at a height R above a horizontal surface. The acceleration due to gravity is g. The block slides along the inside of a frictionless circular hoop of radius R.
Which one of the following expressions gives the speed of the mass at the bottom of the hoop ?
Azero $m / s^{2}$
B $v = \frac{m g}{2 R}$
C $v^{2} = 2 g R$
D $v = m g R$
An object is propelled vertically to a maximum height of 4R from the surface of a planet of radius R and mass M. The speed of object when it returns to the surface of the planet is -
A $2 \sqrt{\frac{2 G M}{5 R}}$
B $\sqrt{\frac{G M}{2 R}}$
C $\sqrt{\frac{3 G M}{2 R}}$
D $\sqrt{\frac{G M}{5 R}}$

NTA MOCK TESTS-NTA JEE MOCK TEST 42-PHYSICS

Home
Ask Doubt
Profile