A stone hanging from a massless string of length 15 m is projected horizontally with speed 12ms−1. The speed of the particle at the point where the tension in the string is equal to the weight of the particle, is close to
10ms−1
7ms−1
12ms−1
5ms−1
The correct Answer is:B
To solve the problem step by step, we will analyze the motion of the stone hanging from the string and apply the principles of physics, particularly the concepts of tension, centripetal force, and conservation of energy.
Step 1: Understanding the Problem
We have a stone hanging from a massless string of length L=15m that is projected horizontally with an initial speed u=12m/s. We need to find the speed v of the stone at the point where the tension in the string equals the weight of the stone.
Step 2: Forces Acting on the Stone
At the point where the tension T in the string equals the weight of the stone mg, we can write:
T=mg
Step 3: Analyzing the Motion
As the stone swings down, it moves in a circular path with radius equal to the length of the string L. The centripetal force required for circular motion is provided by the net force acting towards the center of the circular path.
Step 4: Applying Newton's Second Law
At an angle θ from the vertical, the forces acting on the stone can be resolved into components. The net force towards the center of the circle is given by:
T−mgcosθ=mv2L
Since T=mg, we substitute this into the equation:
mg−mgcosθ=mv2L
Step 5: Simplifying the Equation
Factoring out mg:
mg(1−cosθ)=mv2L
We can cancel m from both sides (assuming m≠0):
g(1−cosθ)=v2L
Step 6: Energy Conservation
We can also apply the principle of conservation of mechanical energy. The initial kinetic energy when the stone is projected is:
KEi=12mu2
As the stone swings down to height h, its potential energy changes. The height h can be expressed as:
h=L−Lcosθ=L(1−cosθ)
The potential energy at height h is:
PE=mgh=mgL(1−cosθ)
The total mechanical energy at the starting point is equal to the total mechanical energy at the point where the tension equals the weight:
12mu2=12mv2+mgL(1−cosθ)
Step 7: Setting Up the Equation
Substituting h into the energy conservation equation:
12m(122)=12mv2+mgL(1−cosθ)
Step 8: Solving for v
We can cancel m from the equation:
12(122)=12v2+gL(1−cosθ)
Substituting g=9.8m/s2 and L=15m:
12(144)=12v2+9.8×15(1−cosθ)
Step 9: Calculate Values
Calculating 9.8×15=147:
72=12v2+147(1−cosθ)
Step 10: Final Calculation
To find v, we can rearrange and solve for v2:
12v2=72−147(1−cosθ)
Assuming θ is small and approximating cosθ≈1, we can simplify further. However, we can also directly calculate v using the earlier derived relationship:
v2=48
v=√48≈6.93m/s
Conclusion
The speed of the stone at the point where the tension in the string equals the weight of the particle is approximately 7m/s.
We have a stone hanging from a massless string of length L=15m that is projected horizontally with an initial speed u=12m/s. We need to find the speed v of the stone at the point where the tension in the string equals the weight of the stone.
At the point where the tension T in the string equals the weight of the stone mg, we can write:
T=mg
As the stone swings down, it moves in a circular path with radius equal to the length of the string L. The centripetal force required for circular motion is provided by the net force acting towards the center of the circular path.
At an angle θ from the vertical, the forces acting on the stone can be resolved into components. The net force towards the center of the circle is given by:
T−mgcosθ=mv2L
mg−mgcosθ=mv2L
Factoring out mg:
mg(1−cosθ)=mv2L
g(1−cosθ)=v2L
We can also apply the principle of conservation of mechanical energy. The initial kinetic energy when the stone is projected is:
KEi=12mu2
h=L−Lcosθ=L(1−cosθ)
PE=mgh=mgL(1−cosθ)
12mu2=12mv2+mgL(1−cosθ)
Substituting h into the energy conservation equation:
12m(122)=12mv2+mgL(1−cosθ)
We can cancel m from the equation:
12(122)=12v2+gL(1−cosθ)
12(144)=12v2+9.8×15(1−cosθ)
Calculating 9.8×15=147:
72=12v2+147(1−cosθ)
To find v, we can rearrange and solve for v2:
12v2=72−147(1−cosθ)
v2=48
v=√48≈6.93m/s
The speed of the stone at the point where the tension in the string equals the weight of the particle is approximately 7m/s.
Topper's Solved these Questions
Similar Questions
A heavy particle hanging from a string of length l is projected horizontally with speed √gl. Find the speed of the particle at the point where the tension in the string equals weight of the particle.
View SolutionA heavy particle hanging from a fixed point by a light inextensible string of length l is projected horizonally with speed √gl . Find the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string is equal to the weight of the particle.
View Solution
Knowledge Check
A stone hanging from a massless string of length 15m is projected horizontally with speed √147ms−1 Then the Speed of the particle, at the point where tension in string equals the weight of particle, is
A10ms−1B7ms−1C12ms−1Dnone of theseA stone hanging from a massless string of length 15m is projected horizontally with speed √147ms−1 Then the Speed of the particle, at the point where tension in string equals the weight of particle, is
A10ms−1B7ms−1C12ms−1Dnone of theseA heavy particle hanging from a fixed point by a light inextensible string of length l is projected horizontally with speed (gl) . Then the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string equal the weight of the particle-
A√31g,cos−1(3/2)B√1g3,cos−1(2/3)C√3g3,cos−1(2/3)D√gl3,cos−1(2/3)
A particle is suspended by a light vertical inelastic string of length 1 from a fixed support. At its equilbrium position it is projected horizontally with a speed √6gl. Find the ratio of the tension in the string in its horizontal position to that in the string when the particle is vertically above the point of support.
View SolutionA heavy particle hanging from a fixed point by a light inextensible string of length l is projected horizonally with speed √gl . Find the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string is equal to the weight of the particle.
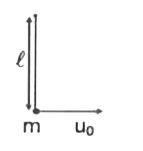
View SolutionThe bob hanging from a light string is projected horizontally with a speed u0. In the subsequent upward motion of the bob in vertically plane
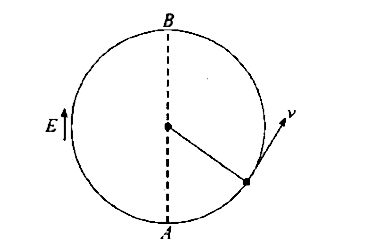
View SolutionA particle of mass m and charge Q is attached to a string of length l. It is whirled in a vertical circle in the region of an electric field E as shown in the figure-5.105.What is the speed given to the particle at the point B,so that tension in the string when the particle is at A is ten times the weight of the particle?
View SolutionA stone of mass m tied to a string of length l is rotated in a circle with the other end of the string as the centre. The speed of the stone is v. If the string breaks, the stone will move
View Solution
