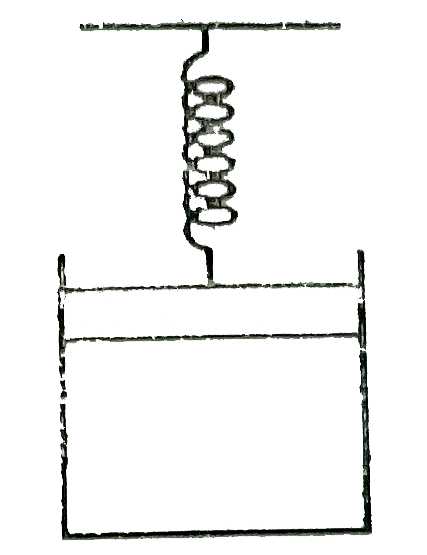
When heat is supplied to the gas it expands and displaces piston by L/2 where natural length of springs are L = 1 m. Spring constant K = 100 N/m. Area of piston is 1m2. The pressure of gas in final situation is

50Nm−2
100Nm−2
200Nm−2
400Nm−2
The correct Answer is:B
Step by step video, text & image solution for When heat is supplied to the gas it expands and displaces piston by L/2 where natural length of springs are L = 1 m. Spring constant K = 100 N/m. Area of piston is 1m^(2). The pressure of gas in final situation is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Block of mass 2m is given v0 towards the right. If L is the natural length of spring constant k, find the maximum elongation of the spring.

View Solution2.00 mol of a monatomic ideal gas (U=1.5nRT) is enclosed in an adiabatic, fixed , vertical cylinder fitted with a smooth, light adiabatic piston.the piston is connected to a vertical spring of spring constant 200Nm−1 as shown in .the area of cross section of the cylinder is 20.0cm2. initially, the spring is at its natural length and the temperature of the gas is at its natural length and the temperature of the gas is 300 K. the atmosphere pressure is 100 kPa. the gas is heated sloewly for some time by means of an electric heater so as to move the poston up through 10 cm. find (a) the work done by the gas (b) the final temperature of the gas and (c ) the heat supplied by the heater.

View Solution
Knowledge Check
The system is released from rest with spring intially in its natural length. If mass of the block m = 10 kg. and spring constant k=100N/m, then maximum extension in spring is :
 A1 mB12mC2 mD2.5 m
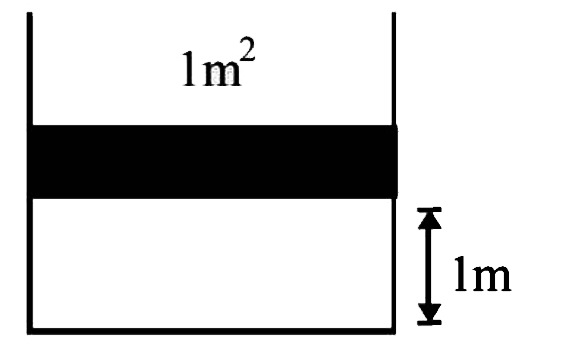
A1 mB12mC2 mD2.5 mOne mole of an ideal gas is kept enclosed under a light piston (area =10−1m2) connected by a compressed spring (spring constant 100 N/m). The volume of gas is 0.83m3 and its temperature is 100K. The gas is heated so that it compresses the spring further by 0.1m. The work done by the gas in the process is : (Take R =8.3J/K-mole and suppose there is no atmosphere).
 A3 JB6 JC9 JD10.5J
A3 JB6 JC9 JD10.5JTwo mole of an ideal monatomic gas are confined within a cylinder by a mass less spring loaded with a frictionless piston of negligible mass and crossectional area 4×10−3m2. The gas is heated by a heater for some time. During this time the gas expands and does 50J of work in moving the piston through a distance of 0.01m. The temperature of gas increases by 50k.
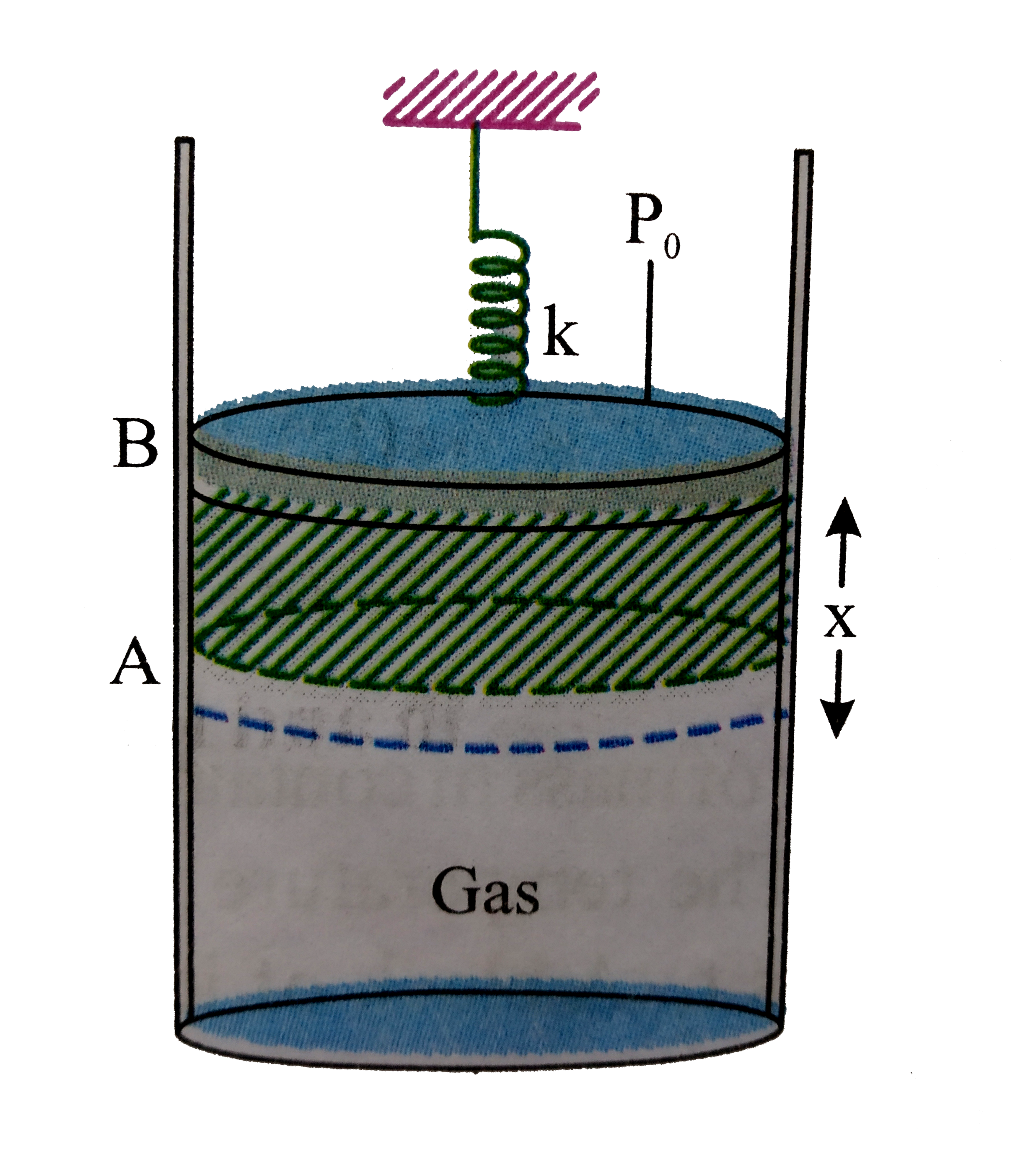
Heat supplied by heater during this process isA129.65JB1296.5JC12.96JD250J
A diatomic gas is enclosed in a vessel fitted with massless movable piston. Area of cross section of vessel is 1m2. Initial height of the piston is 1m (see the figure). The initial temperature of the gas is 300K. The temperature of the gas is increased to 400K, keeping pressure constant, calculate the new height of the piston. The piston is brought to its initial position with no heat exchange. Calculate the final temperature of the gas. You can leave answer in fraction.
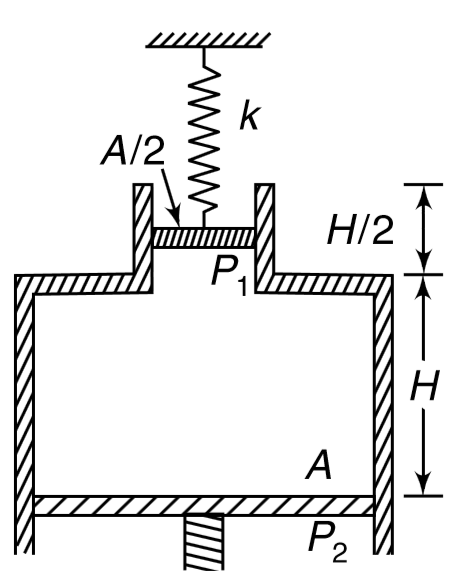
View SolutionIn ideal gas is enclosed in an adiabatic container having cross section A=27cm2 for a part of it and A2 for remaining part. Pistons P1 and P2 can move freely without friction along the inner wall. In the position shown in the figure the spring attached to the piston P1 is relaxed. Sprig constant the spring is K=3700N/m. Piston P2 is pushed up gradually through a distance H2 and its was observed that the piston P1 goes up by 3H32 . Take γ=1.5, mass of piston P1=13.5kg and atmospheric pressure P0=1×105N/m2
(a) Find H.
(b) Find final temperature of the gas if its initial temperature is 300 K.
View SolutionOne mole of an ideal gas is kept enclosed under a light piston (area =10−2m2) connected by a compresses spring (spring constant 100N/m). The volume of gas is 0.83m3 and its temperature is 100K. The gas is heated so that it compresses the spring further by 0.1m. The work done by the gas in the process is N×10−1J. Find N. (Take R=8.3J/K−mole) and suppose there is no atmosphere).
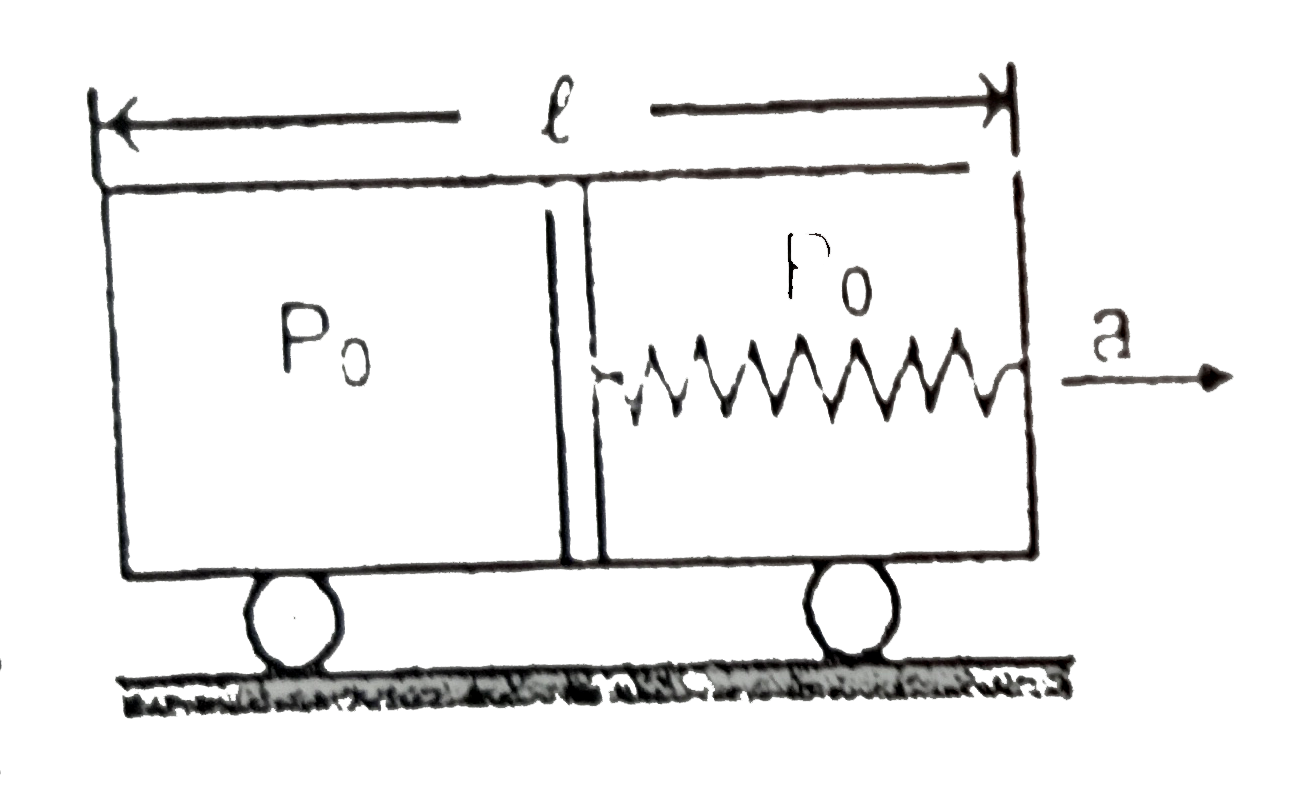
View SolutionAn adiabatic piston of mass m equally divides an insulated container of total volume v0 and length l. A light spring connect the piston to right wall. The container has helium gas. The pressure on both side of piston is P0. The container starts moving with acceleration 'a' towards right, find the stretch of the spring when acceleration of the piston equals acceleration of container. (Assume displacement of the piston <<l)
View SolutionA cylinder of cross-section area. A has two pistons of negligible mass separated by distances l loaded with spring of negligible mass. An ideal gas at temperature T1 is in the cylinder where the springs are relaxed. When the gas is heated by some means its temperature becomes T2 and the springs get compressed by l2 each . if P0 is atmospheric pressure and spring constant k=2P0Al, then find the ratio of T2 and T1 .
_S01_124_Q01.png)
View Solution
